2023-2024学年湖南省长沙一中新华都学校九年级（上）第一次月考数学试卷

一、选择题（在下列各题的四个选项中，只有一个选项是符合题意的。本大题共10个小题，每小题3分，共30分）

• 1．-2023的绝对值是（　　）

  A．-2023

  B． 1 2023

  C． - 1 2023

  D．2023
  组卷：2222引用：157难度：0.9

  解析

• 2．下列四个图案中，是中心对称图形，但不是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：1106引用：22难度：0.9

  解析

• 3．下列计算正确的是（　　）

  A．6a-5a=1	B．a+2a2=3a
  C．-（a-b）=-a+b	D．2（a+b）=2a+b
  组卷：496引用：12难度：0.6

  解析

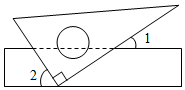• 4．如图，将一块三角尺的直角顶点放在直尺的一边上，当∠1=35°时，∠2的度数为（　　）

  A．35°

  B．45°

  C．55°

  D．65°
  组卷：1508引用：18难度：0.7

  解析

• 5．《义务教育课程标准（2022年版）》首次把学生学会炒菜纳入劳动教育课程，并作出明确规定．某班有7名学生已经学会炒的菜品的种数依次为：2，4，3，2，5，2，3．则这组数据的众数和中位数分别是（　　）

  A．2，2

  B．2，2.5

  C．2，3

  D．3，3
  组卷：553引用：11难度：0.7

  解析

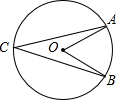• 6．如图，点A、B、C为⊙O上的点，∠AOB=60°，则∠ACB=（　　）

  A．20°

  B．30°

  C．40°

  D．60°
  组卷：631引用：6难度：0.5

  解析

• 7．关于二次函数y=-3（x+1）²+7的图象，下列说法不正确的是（　　）

  A．图象的开口向下

  B．图象的顶点坐标为（-1，7）

  C．图象的对称轴为直线x=1

  D．当x＞0时，y随x的增大而减小
  组卷：192引用：2难度：0.6

  解析

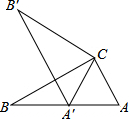• 8．如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕点C顺时针旋转至△A′B′C，使点A′恰好落在AB上，则旋转角度为（　　）

  A．30°

  B．90°

  C．60°

  D．150°
  组卷：781引用：24难度：0.7

  解析

三、解答题（本大题共7个小题，第17、18、19每小题6分，第20、21题每小题6分，第22、23题每小题题9分，第24、25题每小题6分，共72分。解答过程应写出必要的文字说明、证明过程或演算过程）

• 24．约定：若某函数图象上至少存在不同的两点关于直线y=x对称，则把该函数称为“对称函数”，其图象上关于直线y=x对称的两点叫做一对“对称点”．根据该约定，完成下列各题：
  （1）在下列关于x的函数中，是“对称函数”的，请在相应题目后面的横线中打“√”，不是“对称函数”的打“×”．
  ①y=2x

  ；
  ②y=（x-1）²

  ．
  （2）关于x的函数y=kx-2k+2（k是常数）是“对称函数”吗？如果是，写出距离为

  2

  2

  的一对“对称点”坐标；如果不是，请说明理由；
  （3）若关于x的“对称函数”y=ax²+bx+c（a,b,c是常数，a＞0）的一对“对称点”，A、C分别位于x轴、y轴上，求同时满足下列两个条件的“对称函数”的解析式：
  ①该“对称函数”截x轴所得的线段长AB为2；
  ②该“对称函数”截直线y=x所得的线段长MN为

  26

  ．
  组卷：179引用：1难度：0.2

  解析

• 25．如图，二次函数y=（x-1）²+a与x轴相交于点A，B，点A在x轴负半轴，过点A的直线y=x+b交该抛物线于另一点D，交y轴正半轴于点H．
  
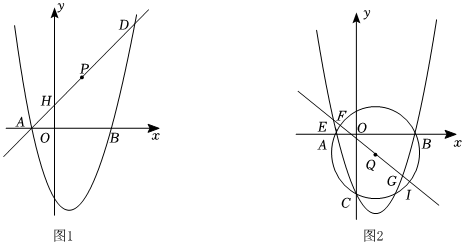
  （1）如图1，若OH=1，求该抛物线的解析式；
  （2）如图1，若点P是线段HD上一点，当

  1

  AH

  +

  1

  AD

  =

  3

  AP

  时，求点P的坐标（用含b的代数式表示）；
  （3）如图2，在（1）的条件下，设抛物线交y轴于点C，过A，B，C三点作⊙Q，经过点Q的直线y=hx+q交⊙Q于点F，I，交抛物线于点E，G．当EI=GI+FI时，求2h²的值．
  组卷：1269引用：2难度：0.1

  解析