2022-2023学年浙江省温州市瑞安中学高二（下）期中数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．若集合A={x∈N^*|x是4和10的公倍数}，B={x∈R|x²≤1000}，则A∩B=（　　）

  A．∅

  B．{-20，20}

  C．{20}

  D．{20，30}
  组卷：48引用：3难度：0.8

  解析

• 2．若复数z满足（z-3）（z-5）+2=0，则

  z

  •

  z

  =（　　）

  A．4

  B． 17

  C．16

  D．17
  组卷：79引用：3难度：0.8

  解析

• 3．已知

  tanα

  =

  1

  2

  ，则

  cosα

  cos

  （

  α

  +

  π

  4

  ）

  =（　　）

  A． - 2 2

  B． - 2

  C． 2

  D． 2 2
  组卷：373引用：4难度：0.8

  解析

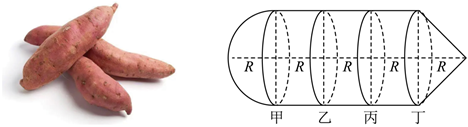
• 4．红薯于1593年被商人陈振龙引入中国，也叫甘薯、番薯等．红薯耐旱耐脊、产量丰富，曾于数次大饥荒年间成为不少人的“救命粮食”，现因其生食多汁、熟食如蜜，成为人们喜爱的美食甜点．小泽和弟弟在网红一条街买了一根香气扑鼻的烤红薯，准备分着吃，如图，该红薯可近似看作三部分：左边部分是半径为R的半球；中间部分是底面半径为R、高为3R的圆柱；右边部分是底面半径为R、高为R的圆锥，若小泽准备从中间部分的甲、乙、丙、丁四个位置选择一处将红薯掰成两块，且使得两块的体积最接近，则小泽选择的位置是（　　）
  

  A．甲

  B．乙

  C．丙

  D．丁
  组卷：60引用：6难度：0.7

  解析

• 5．在△ABC中，AB=2，BC=1，

  ∠

  ABC

  =

  π

  3

  ，若点M满足

  BM

  =

  2

  MA

  ，则

  AM

  •

  AC

  =（　　）

  A． 1 2

  B． 2 3

  C．1

  D． 4 3
  组卷：321引用：4难度：0.7

  解析

• 6．若

  a

  =

  10

  11

  •

  e

  11

  10

  ，

  b

  =

  10

  e

  2

  11

  •

  ln

  11

  10

  ，c=e,则（　　）

  A．b＜c＜a

  B．a＜b＜c

  C．c＜b＜a

  D．a＜c＜b
  组卷：299引用：3难度：0.4

  解析

• 7．已知随机事件A，B，C满足0＜P（A）＜1，0＜P（B）＜1，0＜P（C）＜1，则下列说法错误的是（　　）

  A．不可能事件Φ与事件A互斥

  B．必然事件Ω与事件A相互独立

  C． P （ A | C ） = P （ AB | C ） + P （ A B | C ）

  D．若 P （ A | B ） = P （ A | B ） ，则 P （ A ） = P （ A ） = 1 2
  组卷：458引用：5难度：0.8

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．已知点A（a,-1）是抛物线C：y²=2px（p＞0）上一点，斜率为2的动直线l交C于M，N（异于A）的两点，直线AM，AN的倾斜角互补．
  （1）求抛物线C的方程；
  （2）若|MN|=

  5

  ，求sin∠MAN．
  组卷：130引用：3难度：0.3

  解析

• 22．已知函数f（x）=a^x与g（x）=log_ax（a＞0，且a≠1）．
  （1）求g（x）在（1，g（1））处的切线方程；
  （2）若a＞1，h（x）=f（x）-g（x）恰有两个零点，求a的取值范围．
  组卷：188引用：3难度：0.3

  解析