2022-2023学年湖北省武汉市5G联合体高二（下）期末数学试卷

一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．双曲线

  y

  2

  8

  -

  x

  2

  6

  =

  1

  的一条渐近线方程为（　　）

  A．3x-4y=0

  B．4x-3y=0

  C． 3 x + 2 y = 0

  D． 2 x - 3 y = 0
  组卷：267引用：5难度：0.9

  解析

• 2．已知某质点运动的位移y（单位；cm）与时间t（单位；s）之间的关系为y（t）=ln（2t+1），则该质点在t=2s时的瞬时速度为（　　）

  A． 1 5

  B． 2 5

  C．2

  D．4
  组卷：78引用：5难度：0.8

  解析

• 3．等比数列{a_n}中，a₇=2，a₁₁=8，则a₉=（　　）

  A．±4

  B．±5

  C．4

  D．5
  组卷：253引用：4难度：0.7

  解析

• 4．甲乙两位游客慕名来到赣州旅游，准备分别从大余丫山、崇义齐云山、全南天龙山、龙南九连山和安远三百山5个景点中随机选择其中一个，记事件A：甲和乙选择的景点不同，事件B：甲和乙恰好一人选择崇义齐云山，则条件概率P（B|A）=（　　）

  A． 1 5

  B． 2 5

  C． 9 25

  D． 9 20
  组卷：334引用：9难度：0.8

  解析

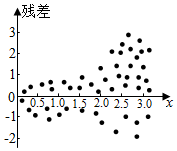• 5．根据变量Y和x的成对样本数据，由一元线性回归模型

  Y = bx + a + e ,

  E （ e ） = 0 ， D （ e ） = σ 2

  得到线性回归模型

  ̂

  y

  =

  ̂

  b

  x

  +

  ̂

  a

  ，对应的残差如图所示，模型误差（　　）

  A．满足一元线性回归模型的所有假设

  B．满足回归模型E（e）=0的假设

  C．满足回归模型D（e）=σ2的假设

  D．不满足回归模型E（e）=0和D（e）=σ2的假设
  组卷：126引用：3难度：0.8

  解析

• 6．设n∊N₊，则5

  C

  1

  n

  +5²

  C

  2

  n

  +5³

  C

  3

  n

  +…+5ⁿ

  C

  n

  n

  除以7的余数为（　　）

  A．0或5

  B．1或3

  C．4或6

  D．0或2
  组卷：406引用：7难度：0.9

  解析

• 7．已知定义域为R的奇函数f（x）的图象是一条连续不断的曲线，当x∈（2，+∞）时，f′（x）＜0，当x∈（0，2）时，f′（x）＞0，且f（3）=0，则关于x的不等式（x-1）f（x）＞0的解集为（　　）

  A．（-3，3）	B．（-3，0）∪（0，3）
  C．（-3，0）∪（1，3）	D．（-∞，-3）∪（0，3）
  组卷：157引用：6难度：0.5

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．从甲、乙、丙等5人中随机地抽取三个人去做传球训练．训练规则是确定一人第一次将球传出，每次传球时，传球者都等可能地将球传给另外两个人中的任何一人，每次必须将球传出．
  （1）记甲乙丙三人中被抽到的人数为随机变量X，求X的分布列；
  （2）若刚好抽到甲乙丙三个人相互做传球训练，且第1次由甲将球传出，记n次传球后球在甲手中的概率为p_n，n=1，2，3，⋯，
  ①直接写出p₁，p₂，p₃的值；
  ②求p_n+1与p_n的关系式（n∈N^*），并求p_n（n∈N^*）．
  组卷：631引用：7难度：0.5

  解析

• 22．已知椭圆

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的离心率为

  1

  2

  ，左、右焦点分别为F₁，F₂，直线x=m与椭圆C交于A，B两点，且△ABF₁的周长最大值为8．
  （1）求椭圆C的标准方程；
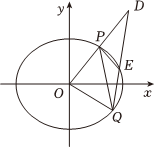
  （2）如图，P，Q是椭圆C上的两点，且直线OP与OQ的斜率之积为

  -

  3

  4

  （O为坐标原点），D为射线OP上一点，且|OP|=|PD|，线段DQ与椭圆C交于点E，

  |

  QE

  |

  =

  2

  3

  |

  ED

  |

  ，求四边形OPEQ的面积．
  组卷：280引用：3难度：0.1

  解析