2022-2023学年辽宁省辽东区域教育科研共同体高一（下）期中数学试卷

一、选择题（本题共8小题，每小题5分，共40分，在每个小题给出的四个选项中，只有一项是符合题目要求）

• 1．点P（tan2023°，cos2023°）位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：207引用：2难度：0.8

  解析

• 2．已知

  sinα

  =

  3

  5

  ，且α为第二象限角，则

  sinα

  +

  cosα

  sinα

  -

  2

  cosα

  的值为（　　）

  A． - 1 11

  B． 1 11

  C． - 7 5

  D． 7 5
  组卷：661引用：7难度：0.8

  解析

• 3．已知向量

  |

  a

  |=2，

  |

  b

  |=1，且

  |

  a

  -

  3

  b

  |

  =

  7

  ，则向量

  a

  ，

  b

  的夹角是（　　）

  A． 5 π 6

  B． π 6

  C． 2 π 3

  D． π 3
  组卷：1048引用：9难度：0.8

  解析

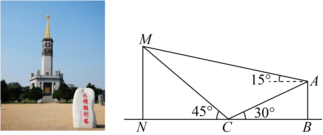• 4．胜利塔位于大连市旅顺口区，是市级文物保护单位．该塔是苏军撤离旅顺之前，为纪念世界反法西斯战争胜利10周年而建．基座为五角形，五面各有二层台阶，上立有五根六角柱，中心为五角形的塔身，其顶端铸有象征胜利的红色徽标，金碧辉煌，格外耀眼．某同学为测量胜利塔的高度MN，在胜利塔的正北方向找到一座建筑物AB，高约为22.5m,在地面上点C处（B，C，N三点共线）测得建筑物顶部A，胜利塔顶部M的仰角分别为30°和45°，在A处测得胜利塔顶部M的仰角为15°，那么胜利塔的高度约为（　　）

  A．32m

  B．39m

  C．45m

  D．55m
  组卷：45引用：4难度：0.6

  解析

• 5．要得到

  y

  =

  cos

  2

  x

  -

  3

  sin

  2

  x

  的图象，可将函数y=-4sinxcosx的图象（　　）

  A．向左平移 π 12 个单位长度

  B．向右平移 π 12 个单位长度

  C．向左平移 π 6 个单位长度

  D．向右平移 π 6 个单位长度
  组卷：72引用：2难度：0.7

  解析

• 6．已知△ABC中，角A，B，C的对边分别为a,b,c,且a=csinB+bcosC，b=4，则

  a

  -

  c

  sin

  A

  -

  sin

  C

  =（　　）

  A．4

  B．6

  C． 4 2

  D． 6 2
  组卷：177引用：3难度：0.6

  解析

• 7．已知

  a

  =

  2

  sin

  1

  2

  ，

  b

  =

  2

  sin

  1

  4

  ，

  c

  =

  cos

  1

  4

  ，则（　　）

  A．c＜b＜a

  B．b＜c＜a

  C．a＜b＜c

  D．b＜a＜c
  组卷：48引用：2难度：0.6

  解析

四、解答题（本题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤）

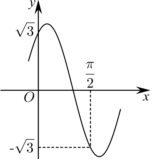• 21．已知函数

  f

  （

  x

  ）

  =

  A

  sin

  （

  ωx

  +

  φ

  ）

  （

  A

  ＞

  0

  ，

  ω

  ＞

  0

  ，

  |

  φ

  |

  ＜

  π

  2

  ）

  的部分图象如图所示，且直线

  x

  =

  π

  12

  为f（x）图象的一条对称轴．
  （1）求f（x）的解析式；
  （2）若方程

  f

  （

  x

  -

  π

  4

  ）

  -

  m

  =

  0

  在区间

  [

  0

  ，

  π

  2

  ）

  上有且仅有1个实数根，求m的取值范围．
  组卷：159引用：2难度：0.5

  解析

• 22．△ABC中，角A，B，C的对边分别是a,b,c,b=1，cos²A-cos²B+cos²C=1．
  （1）求△ABC面积的最大值；
  （2）若

  AB

  •

  AC

  ＜

  1

  2

  ，求

  1

  a

  +

  1

  c

  的取值范围．
  组卷：68引用：3难度：0.5

  解析