2022-2023学年江苏省常州市联盟学校高一(下)学情调研数学试卷(3月份)
发布:2024/7/19 8:0:9
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知向量
=(4,2),a=(x,3),且b∥a,则x等于( )b组卷:489引用:16难度:0.9 -
2.sin160°cos10°+cos20°sin10°=( )
组卷:202引用:18难度:0.9 -
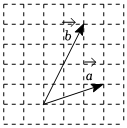 3.已知向量,a在正方形网格中的位置如图所示,那么向量b与a-b的夹角为( )b组卷:61引用:3难度:0.8
3.已知向量,a在正方形网格中的位置如图所示,那么向量b与a-b的夹角为( )b组卷:61引用:3难度:0.8 -
4.密位制是度量角的一种方法,把一周角等分为6000份,每一份叫做1密位的角.在角的密位制中,单位可省去不写,采用四个数码表示角的大小,在百位数与十位数之间画一条短线,如7密位写成“0-07”,478密位写成“4-78”.如果一个半径为4的扇形,其圆心角用密位制表示为6-25,则该扇形的面积为( )
组卷:34引用:2难度:0.8 -
5.已知A(-3,0),B(0,2),O为坐标原点,点C在∠AOB内,|
|=2OC,且∠AOC=2,设π4=OC+λOA(λ∈R),则λ的值为( )OB组卷:118引用:8难度:0.7 -
6.在平面直角坐标系xOy中,α为第四象限角,角α的终边与单位圆O交于点P(x0,y0),若
,则y0=( )cos(α-π3)=-33组卷:35引用:3难度:0.7 -
7.已知A是函数
的最大值,若存在实数x1,x2使得对任意实数x总有f(x1)≤f(x)≤f(x2)成立,则A|x1-x2|的最小值为( )f(x)=3sin(2023x+π4)+sin(2023x-π4)组卷:95引用:3难度:0.7
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.已知梯形ABCD中,
,AB=BC=2,∠ABC=60°,E为BC的中点,连接AE.AB=2DC
(1)若,求证:B,F,D三点共线;AF=4FE
(2)求与AE所成角的余弦值;BD
(3)若P为以B为圆心、BA为半径的圆弧(包含A,C)上的任意一点,当点P在圆弧ˆAC(包含A,C)上运动时,求ˆAC的最小值.PA•PC组卷:98引用:3难度:0.6 -
22.已知向量
,a=(cosx,cos2x).设函数b=(sin(x+π6),-1),x∈R.f(x)=2a•b+12
(1)求函数f(x)的解析式及其单调增区间;
(2)设,若方程2g(x)-m=1在g(x)=f(x+π4)上有两个不同的解x1,x2,求实数m的取值范围,并求tan(x1+x2)的值.x∈[0,π2]
(3)若将y=f(x)的图像上的所有点向左平移个单位,再把所得图像上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到函数h(x)的图像.当π4(其中m∈[0,π])时,记函数h(x)的最大值与最小值分别为h(x)max与h(x)min,设φ(m)=h(x)max-h(x)min,求函数φ(m)的解析式.x∈[m,m+π2]组卷:88引用:4难度:0.6


