2022-2023学年湖南省湘潭市、衡阳市、邵阳市三市教研联考高一（下）期中数学试卷

一、单选题（本大题共8小题，共40分。在每小题列出的选项中，选出符合题目的一项）

• 1．已知复数z满足（1+i）z=3-i,则z的虚部为（　　）

  A．2

  B．-2

  C．2i

  D．-2i
  组卷：36引用：2难度：0.8

  解析

• 2．已知a＞0，b＞0，且a+2b=1，则

  1

  a

  +

  1

  b

  的最小值为（　　）

  A． 2

  B． 1 2

  C．3-2 2

  D．3+2 2
  组卷：364引用：7难度：0.8

  解析

• 3．已知正六边形ABCDEF中，

  AB

  +

  CD

  +

  EF

  =（　　）

  A． AF

  B． BE

  C． CD

  D． 0
  组卷：1027引用：3难度：0.7

  解析

• 4．设a=lg2，b=cos2，c=2^0.2，则（　　）

  A．b＜c＜a

  B．c＜b＜a

  C．b＜a＜c

  D．a＜b＜c
  组卷：717引用：13难度：0.8

  解析

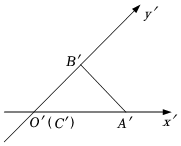• 5．如图，水平放置的△ABC的斜二测直观图是图中的△A'B'C'，若A'C'=2，A'B'=2，则△ABC的面积为（　　）

  A． 2 2

  B． 4 2

  C．8

  D． 8 2
  组卷：220引用：3难度：0.8

  解析

• 6．函数

  f

  （

  x

  ）

  =

  1

  2

  x

  -

  lo

  g

  2

  x

  +

  1

  的零点所在区间为（　　）

  A．（0，1）

  B．（1，2）

  C．（2，3）

  D．（3，4）
  组卷：181引用：6难度：0.7

  解析

• 7．若△ABC为锐角三角形，则（　　）

  A．sinA＞sinB	B．cosA＞cosB
  C．sin（cosA）＞sin（sinB）	D．cos（cosA）＞cos（sinB）
  组卷：78引用：3难度：0.6

  解析

四、解答题（本大题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤）

• 21．对于函数f（x），g（x），若存在实数k使得函数h（x）=kf（x）•g（x），那么称函数h（x）为f（x），g（x）的k积函数．
  （1）设函数f（x）=sinx,

  g

  （

  x

  ）

  =

  cos

  （

  x

  +

  2

  π

  3

  ）

  ，

  h

  （

  x

  ）

  =

  2

  sin

  （

  2

  x

  -

  π

  3

  ）

  +

  3

  ，试判断h（x）是否为f（x），g（x）的k积函数？若是，请求出k的值；若不是，请说明理由；
  （2）设函数

  f

  （

  x

  ）

  =

  mx

  +

  n

  x

  （其中m＞0，n＞0，x＞0），且函数f（x）图象的最低点坐标为（2，4），若函数g（x）=f（2-x），h（x）是f（x），g（x）的1积函数，且对于任意实数x∈（0，2），h（x）≥a恒成立，求实数a的取值范围．
  组卷：32引用：3难度：0.5

  解析

• 22．在①（a+c）（sinA-sinC）=b（sinA-sinB）；②

  2

  b

  -

  a

  c

  -

  cos

  A

  cos

  C

  =

  0

  ；③向量

  m

  =

  （

  c

  ,

  3

  b

  ）

  与

  n

  =

  （

  cos

  C

  ，

  sin

  B

  ）

  平行，这三个条件中任选一个，补充在下面题干中，然后解答问题．
  已知△ABC内角A，B，C的对边分别为a,b,c,且满足_______．
  （1）求角C；
  （2）若△ABC为锐角三角形，且a=4，求△ABC面积的取值范围．
  组卷：282引用：5难度：0.5

  解析