2023年湖北省荆门市龙泉中学高考数学模拟试卷(5月份)
发布:2024/5/8 8:0:8
一、单项选择题:本题共8小题,每小题5分,共40分.出的四个选项中,只有一项是符合题目要求的.
-
1.已知集合A={a,5-a,4},B={3,2a+1},A∪B={2,3,4,5},则a=( )
组卷:64引用:3难度:0.7 -
2.已知复数iz=1+5i,则复数
=( )z+z组卷:53引用:3难度:0.9 -
3.已知双曲线C:
的一条渐近线与直线2x-y+1=0垂直,则该双曲线C的离心率为( )x2a2-y2b2=1(a>0,b>0)组卷:213引用:3难度:0.7 -
4.某人周一至周五每天6:30至6:50出发去上班,其中在6:30至6:40出发的概率为0.4,在该时间段出发上班迟到的概率为0.1;在6:40至6:50出发的概率为0.6,在该时间段出发上班迟到的概率为0.2,则小王某天在6:30至6:50出发上班迟到的概率为( )
组卷:147引用:2难度:0.7 -
5.已知点O为△ABC所在平面内一点,在△ABC中,满足
,2AB•AO=|AB|2,则点O为该三角形的( )2AC•AO=|AC|2组卷:171引用:6难度:0.7 -
6.一个四棱锥的四个侧面中,钝角三角形最多有( )
组卷:57引用:2难度:0.5 -
7.在我国古代,杨辉三角(如图1)是解决很多数学问题的有力工具,从图1中可以归纳出等式:
、类比上述结论,借助杨辉三角解决下述问题:如图2,该“刍童垛”共2021层,底层如图3,一边2023个圆球,另一边2022个圆球,向上逐层每边减少1个圆球,顶层堆6个圆球,则此“刍童垛”中圆球的总数为( )C11+C12+C13+⋯+C1n=C2n+1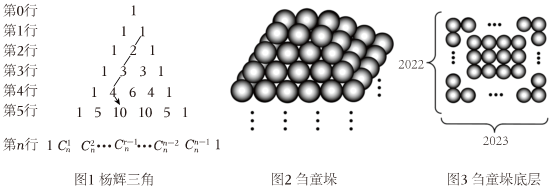 组卷:89引用:5难度:0.7
组卷:89引用:5难度:0.7
四、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.
-
21.设函数f(x)=ex-ax,x≥0且a∈R.
(1)求函数f(x)的单调性;
(2)若f(x)≥x2+1恒成立,求实数a的取值范围.组卷:365引用:8难度:0.4 -
22.已知椭圆E:
.若直线l:x24+y22=1与椭圆E交于A、B两点,交x轴于点F,点A,F,B在直线l′:x=my+2上的射影依次为点D,K,G.x=22
(1)若直线l交y轴于点T,且,TA=λ1AF,当m变化时,探究λ1+λ2的值是否为定值?若是,求出λ1+λ2的值;否则,说明理由;TB=λ2BF
(2)连接AG,BD,试探究当m变化时,直线AG与BD是否相交于定点?若是,请求出定点的坐标,并给予证明:否则,说明理由.组卷:49引用:2难度:0.5


