当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省无锡市四校联考高一（下）期中数学试卷

发布：2024/8/27 4:0:8

一、单选题（本大题共8小题，每小题只有一个正确选项，每题5分，共40分）

1．已知复数
z
=
2
+
i
1
-
i
，则z•
z
=（　　）
A．1 B．
3
2
C．2 D．
5
2
组卷：65引用：2难度：0.8
解析
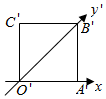2．一个水平放置的平面图形，用斜二测画法画出了它的直观图，如图所示，此直观图恰好是一个边长为2的正方形，则原平面图形的面积为（　　）
A．
2
B．
4
2
C．8 D．
8
2
组卷：441引用：5难度：0.8
解析
3．一质点在力
F
1
=（-3，5），
F
2
=（2，-3）的共同作用下，由点A（10，-5）移动到B（4，0），则
F
1
，
F
2
的合力
F
对该质点所做的功为（　　）
A．16 B．-24 C．110 D．-110
组卷：197引用：3难度：0.8
解析
4．在△ABC中，a²+b²+c²=2bccosA+2accosB，则△ABC一定是（　　）
A．锐角三角形 B．钝角三角形 C．直角三角形 D．等边三角形
组卷：236引用：3难度：0.8
解析
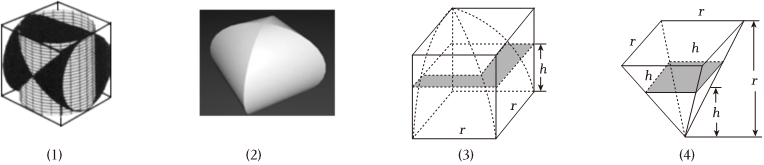
5．中国古代数学家刘徽在《九章算术注》中，称一个正方体内两个互相垂直的内切圆柱所围成的立体为“牟合方盖”，如图（1）（2），刘徽未能求得牟合方盖的体积，直言“欲陋形措意，惧失正理”，不得不说“敢不阙疑，以俟能言者”．约200年后，祖冲之的儿子祖暅提出“幂势既同，则积不容异”，后世称为祖暅原理，即：两等高立体，若在每一等高处的截面积都相等，则两立体体积相等．如图（3）（4），祖暅利用八分之一正方体去掉八分之一牟合方盖后的几何体与长宽高皆为八分之一正方体的棱长的倒四棱锥“等幂等积”，计算出牟合方盖的体积，据此可知，牟合方盖的体积与其外切正方体的体积之比为（　　）
A．
1
3
B．
2
3
C．
8
3
D．
16
3
组卷：171引用：5难度：0.7
解析
6．已知
α
∈
（
0
，
π
2
）
，
sin
2
α
=
cos
（
π
4
-
α
）
，则cos2α的值为（　　）
A．0 B．
1
2
C．
3
2
D．-
3
2
组卷：299引用：5难度：0.6
解析
7．设A₁、A₂、A₃、A₄为平面直角坐标系中两两不同的点，若
A
1
A
3
=
λ
A
1
A
2
（
λ
∈
R
）
，
A
1
A
4
=
μ
A
1
A
2
（
μ
∈
R
）
，且
1
λ
+
1
μ
=
4
，则称点A₃、A₄和谐分割点A₁、A₂.已知平面上两两不同的点A、B、C、D，若C、D和谐分割点A、B．则下面说法正确的是（　　）
A．点C可能是线段AB的中点
B．点C可能是靠近点A的线段AB的三等分点
C．点C、D可能同时在线段AB上
D．点C、D可能同时在线段AB的延长线上
组卷：127引用：3难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共6小题，作答各题时须有必要的计算和推理过程，共70分）

21．如图所示，在△ABC中，P在线段BC上，满足2
BP
=
PC
，O是线段AP的中点，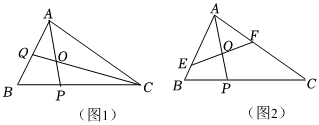

（1）延长CO交AB于点Q（图1），求
AQ
QB
的值；
（2）过点O的直线与边AB，AC分别交于点E，F（图2），设
EB
=
λ
AE
，
FC
=
μ
AF
．
（ⅰ）求证：2λ+μ为定值；
（ⅱ）设△AEF的面积为S₁，△ABC的面积为S₂，求
S
1
S
2
的最小值．
组卷：613引用：5难度：0.2
解析
22．如图，某公园改建一个三角形池塘，∠C=90°，AB=2百米，BC=1百米，现准备养一批观赏鱼供游客观赏．

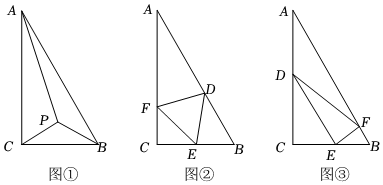
（1）若在△ABC内部取一点P，建造连廊供游客观赏，方案一如图①，使得点P是等腰三角形PBC的顶点，且
∠
CPB
=
2
π
3
，求连廊AP+PC+PB的长（单位为百米）；
（2）若分别在AB，BC，CA上取点D，E，F，并建造连廊，使得△DEF变成池中池，放养更名贵的鱼类供游客观赏：方案二如图②，使得△DEF为正三角形，设S₂为图②中△DEF的面积，求S₂的最小值；方案三如图③，使得DE平行于AB，且EF垂直于DE，设S₃为图③中△DEF的面积，求S₃的取值范围．
组卷：153引用：4难度：0.7
解析