2023-2024学年贵州省贵阳市第三实验中学高一(上)月考数学试卷(一)
发布:2024/10/2 6:0:2
一、选择题(本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求)
-
1.若命题p:∃x>0,x2-3x+2>0,则命题¬p为( )
组卷:201引用:21难度:0.9 -
2.全集U={1,2,3,4,5,6,7,8},A={1,2,3},B={1,2,7,8},则(∁UA)∩B=( )
组卷:343引用:16难度:0.8 -
3.二次不等式ax2+bx+c<0的解集是(2,3),则
的值为( )cb组卷:672引用:4难度:0.7 -
4.若函数f(x)=x2-mx+10在(-2,-1)上是减函数,则实数m的取值范围是( )
组卷:442引用:7难度:0.7 -
5.“x>y>0”是“
”的( )x-1x>y-1y组卷:354引用:8难度:0.7 -
6.某班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形、三角形、弓形这三种方案,最佳方案是( )
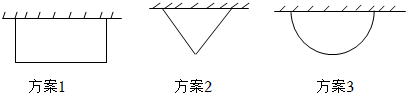 组卷:31引用:3难度:0.8
组卷:31引用:3难度:0.8 -
7.若不等式x2+a(x-1)+1≥0对一切x∈(1,2]都成立,则a的最小值为( )
组卷:83引用:3难度:0.6
四、解答题:共68分.解答应写出文字说明、证明过程或演算步骤.
-
21.已知二次函数y=ax2+bx+c的顶点坐标为(2,-5),且过点(0,-1).
(1)求a、b、c的值;
(2)设u=(a-p)x2+(b+q)x+c+2,不等式u>0的解集为,对∀x>1,3λx2+(u-2)λ-2≤x2-3λx恒成立,求λ的取值范围?{x|-1<x<13}组卷:111引用:1难度:0.3 -
22.函数y=f(x)的定义域为R,若存在常数M>0,使得|f(x)|≥M|x|对一切实数x均成立,则称f(x)为“圆锥托底型”函数.
(1)判断函数f(x)=2x,g(x)=x3是否为“圆锥托底型”函数?并说明理由.
(2)若f(x)=x2+1是“圆锥托底型”函数,求出M的最大值.
(3)问实数k、b满足什么条件,f(x)=kx+b是“圆锥托底型”函数.组卷:244引用:6难度:0.1


