2022-2023学年湖南省长沙一中高三（下）月考数学试卷（八）

一、单项选择题（本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）

• 1．已知集合A={x|x²＜2x}，集合B={x|log₂（x-1）＜1}，则A∩B=（　　）

  A．{x|0＜x＜3}

  B．{x|1＜x＜2}

  C．{x|2≤x＜3}

  D．{x|0＜x＜2}
  组卷：116引用：5难度：0.8

  解析

• 2．在复平面内，复数z与

  2

  1

  -

  i

  对应的点关于虚轴对称，则z等于（　　）

  A．1+i

  B．-1-i

  C．1-i

  D．-1+i
  组卷：95引用：5难度：0.8

  解析

• 3．若双曲线

  C

  ：

  x

  2

  9

  -

  y

  2

  b

  =

  1

  （

  b

  ＞

  0

  ）

  的一条渐近线与x轴的夹角是

  π

  3

  ，则C的虚轴长是（　　）

  A． 6 3

  B． 3 3

  C．2

  D． 2 3 3
  组卷：19引用：3难度：0.7

  解析

• 4．若（1+x）（1-2x）⁷=a₀+a₁x+a₂x²+⋯+a₈x⁸．则a₁+a₃+a₅+a₇的值是（　　）

  A．-1

  B．-2

  C．2

  D．1
  组卷：95引用：1难度：0.7

  解析

• 5．在△ABC中，“cosA+sinA=cosB+sinB”是“∠C=90°”的（　　）

  A．充分非必要条件	B．必要非充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：664引用：3难度：0.9

  解析

• 6．长沙烈士公园西南小丘上兴建了烈士纪念塔，纪念为人民解放事业牺牲的湖南革命烈士，它是公园的标志．为了测量纪念塔的实际高度，某同学设计了如下测量方案：在烈士纪念塔底座平面的A点位置测得纪念塔顶端仰角的正切值为

  3

  2

  ，然后直线走了20m,抵达纪念塔底座平面B点位置测得纪念塔顶端的仰角为

  π

  3

  ．已知该同学沿直线行进的方向与他第一次望向烈士纪念塔底端的方向所成角为

  π

  3

  ，则该烈士纪念塔的高度约为（　　）

  A．30m

  B．45m

  C．60m

  D．75m
  组卷：16引用：2难度：0.7

  解析

• 7．已知点P（2，2），直线AB与抛物线C：y²=2x交于A、B两点，且直线PA，PB的倾斜角互补，则直线AB的斜率为（　　）

  A． - 1 4

  B． - 1 2

  C．-1

  D．-2
  组卷：66引用：2难度：0.6

  解析

四、解答题（本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）

• 21．已知f（x）=e^x-tx,x∈R．
  （1）函数f（x）有且仅有一个零点，求t的取值范围．
  （2）当t=1时，证明：∃ξ∈（a,b）（其中a＞0），使得

  f

  （

  b

  ）

  -

  f

  （

  a

  ）

  b

  -

  a

  =

  e

  ξ

  -

  1

  ．
  组卷：52引用：3难度：0.6

  解析

• 22．历史上第一个研究圆锥曲线的是梅纳库莫斯（公元前375年—公元前325年），大约100年后，阿波罗尼斯更详尽、系统地研究了圆锥曲线，并且他还进一步研究了这些圆锥曲线的光学性质：如图，从椭圆的一个焦点出发的光线或声波，经椭圆反射后，反射光线经过椭圆的另一个焦点，其中法线l'表示与椭圆C的切线垂直且过相应切点的直线，已知椭圆C的中心在坐标原点，焦点为F₁（-c,0），F₂（c,0）（c＞0），若由F₁发出的光线经椭圆两次反射后回到F₁经过的路程为8c.对于椭圆C上除顶点外的任意一点P，椭圆在点P处的切线为l,F₁在l上的射影为H，其中

  |

  OH

  |

  =

  2

  2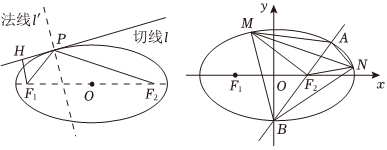

  ．
  
  （1）求椭圆C的方程；
  （2）如图，过F₂作斜率为k（k＞0）的直线m与椭圆C相交于A，B两点（点A在x轴上方）．点M，N是椭圆上异于A，B的两点，MF₂，NF₂分别平分∠AMB和∠ANB，若△MF₂N外接圆的面积为

  81

  π

  8

  ，求直线m的方程．
  组卷：93引用：2难度：0.5

  解析