当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省南京二十七中高一（上）期中数学试卷

发布：2024/9/13 1:0:8

一、单选题（本大题共8小题，共40分。在每小题列出的选项中，选出符合题目的一项）

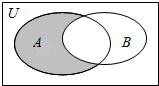1．设全集U={1，2，3，4，5，6}，A={1，2}，B={2，3，4}，则图中阴影部分表示的集合为（　　）
A．{1，2，5，6} B．{1} C．{2} D．{1，2，3，4}
组卷：89引用：5难度：0.9
解析
2．下列函数中，在区间（0，2）上是增函数的是（　　）
A．y=-x+1 B．y=x²-4x+5 C．
y
=
x
D．
y
=
1
x
组卷：219引用：3难度：0.8
解析
3．已知集合A={a+1，a²+4a-9，2021}，若-4∈A，则实数a的值为（　　）
A．-5 B．1 C．5或-1 D．-5或1
组卷：481引用：2难度：0.7
解析
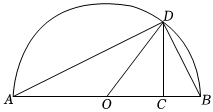4．《几何原本》卷2的几何代数法（用几何方法研究代数问题）成了后世西方数学家处理问题的重要依据，通过这一原理，很多代数公理、定理都能够通过图形实现证明，并称之为“无字证明“．”现有如图形：AB是半圆O的直径，点D在半圆周上，CD⊥AB于点C，设AD=a,BD=b,直接通过比较线段OD与线段CD的长度可以完成的“无字证明”为（　　）
A．a²+b²≥2ab B．
a
2
+
b
2
2
≥
a
+
b
2
C．
2
ab
a
+
b
≤
ab
（
a
＞
0
，
b
＞
0
）
D．
a
+
b
2
≥
ab
（
a
＞
0
，
b
＞
0
）
组卷：310引用：3难度：0.6
解析
5．二次函数f（x）=x²-2x+2在[-2，2]的值域为（　　）
A．[1，2] B．[2，8] C．[2，10] D．[1，10]
组卷：78引用：2难度：0.7
解析
6．设集合M={x|0≤x≤2}，N={y|0≤y≤3}．下列四个图象中能表示从集合M到集合N的函数关系的有（　　）
A．3个 B．2个 C．1个 D．0个
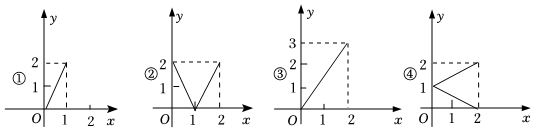组卷：119引用：3难度：0.7
解析
7．已知命题p：∀x∈R，x²+x+a≠0，若命题p是假命题，则实数a的取值范围是（　　）
A．
{
a
|
a
≤
1
4
}
B．
{
a
|
a
＜
1
4
}
C．
{
a
|
a
＜
1
4
或
a
＞
0
}
D．
{
a
|
a
≤
1
4
或
a
≥
0
}
组卷：154引用：4难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤）

21．某企业采用新工艺，把企业生产中排放的二氧化碳转化为一种可利用的化工产品．已知该单位每月的处理量最少为300吨，最多为600吨，月处理成本y（元）与月处理量x（吨）之间的函数关系可近似地表示为y=
1
2
x
2
-200x+80000，且每处理一吨二氧化碳得到可利用的化工产品价值为100元．
（1）该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低？
（2）该单位每月能否获利？如果获利，求出最大利润；如果不获利，则国家至少需要补贴多少元才能使该单位不亏损？
组卷：612引用：33难度：0.6
解析
22．对于定义域为D的函数f（x），若同时满足下列两个条件：①f（x）在D上具有单调性；②存在区间[a,b]⊆D，使f（x）在区间[a,b]上的值域也为[a,b]，则称f（x）为D上的“精彩函数”，区间[a,b]为函数f（x）的“精彩区间”．
（1）判断[0，1]是否为函数y=x³的“精彩区间”，并说明理由；
（2）判断函数f（x）=x+
4
x
（
x
＞
0
）
是否为“精彩函数”，并说明理由；
（3）若函数g（x）=
x
+
4
+m是“精彩函数”，求实数m的取值范围．
组卷：216引用：3难度：0.6
解析