2022-2023学年河北省保定市河北安国中学等高三（上）期中数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．（3-2i）（2-i）=（　　）

  A．8+7i

  B．8-7i

  C．4+7i

  D．4-7i
  组卷：33引用：6难度：0.8

  解析

• 2．已知集合A={2，3，5，7，9}，B={1，2，3，5，7}，则A∩B的真子集的个数为（　　）

  A．7

  B．8

  C．15

  D．16
  组卷：320引用：4难度：0.8

  解析

• 3．“x²-3x＜10”是“

  1

  4

  ＜

  2

  x

  ＜

  31

  ”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：3引用：2难度：0.8

  解析

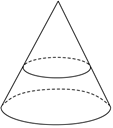• 4．已知某种装水的瓶内芯近似为底面半径是4dm、高是8dm的圆锥，当瓶内装满水并喝完一半，且瓶正立放置时（如图所示），水的高度约为（　　）
  （参考数据：

  3

  3

  ≈

  1

  .

  44

  ，

  3

  4

  ≈

  1

  .

  59

  ）

  A．1.62dm

  B．1.64dm

  C．3.18dm

  D．3.46dm
  组卷：52引用：7难度：0.7

  解析

• 5．已知函数

  f

  （

  x

  ）

  =

  1

  +

  2

  sin

  （

  2

  x

  +

  π

  3

  ）

  中，则（　　）

  A．f（x）的最大值为2

  B．直线 x = - π 12 是f（x）图象的一条对称轴

  C．点 （ π 3 ， 0 ） 是f（x）图象的一个对称中心

  D．f（x）在 （ π 12 ， 7 π 12 ） 上单调递减
  组卷：291引用：4难度：0.5

  解析

• 6．若2＜m＜8，椭圆C：

  x

  2

  m

  +

  y

  2

  2

  =

  1

  与椭圆D：

  x

  2

  m

  +

  y

  2

  8

  =

  1

  的离心率分别为e₁，e₂，则（　　）

  A．e1•e2的最小值为 3 2	B．e1•e2的最小值为 1 2
  C．e1•e2的最大值为 3 2	D．e1•e2的最大值为 1 2
  组卷：143引用：7难度：0.7

  解析

• 7．南宋数学家在《详解九章算法》和《算法通变本末》中提出了一些新的垛积公式，所讨论的高阶等差数列与一般等差数列不同，高阶等差数列中前、后两项之差并不相等，但是逐项差数之差或者高次差成等差数列．现有一高阶等差数列，其前7项分别为1，2，4，7，11，16，22，则该数列的第20项为（　　）

  A．183

  B．125

  C．162

  D．191
  组卷：109引用：6难度：0.8

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知A（-1，0），B（1，0），动点C满足直线AC与直线BC的斜率乘积为3．记动点C的轨迹为E．
  （1）求E的方程；
  （2）过点（2，0）作直线l₁交E于P，Q两点（P，Q在y轴两侧），过原点O作直线l₁的平行线l₂交E于M，N两点（M，N在y轴两侧），试问

  |

  MN

  |

  2

  |

  PQ

  |

  是否为定值？若是，求出该定值；若不是，请说明理由．
  组卷：13引用：1难度：0.4

  解析

• 22．设g′（x）为g（x）的导函数，若g′（x）是定义域为D的增函数，则称g（x）为D上的“凹函数”．已知函数f（x）=xe^x+ax²+a为R上的凹函数．
  （1）求a的取值范围；
  （2）证明：

  f

  （

  x

  ）

  ＞

  1

  2

  x

  3

  +

  45

  44

  x

  2

  +

  x

  +

  1

  44

  ．
  组卷：3引用：3难度：0.5

  解析