2022-2023学年广东省梅州市丰顺县东留中学八年级(上)月考数学试卷(12月份)
发布:2024/8/26 4:0:8
一、选择题(共10题,共30分)
-
1.已知a>0,b<0,那么点P(a,b)在( )
组卷:474引用:29难度:0.9 -
2.下列各组线段中,不能构成三角形的是( )
组卷:11引用:1难度:0.7 -
3.关于x的方程kx+b=3的解为x=7,则直线y=kx+b的图象一定过点( )
组卷:3542引用:12难度:0.7 -
 4.甲、乙两车从A地出发,沿同一路线驶向B地.甲车先出发匀速驶向B地,40min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地.甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:
4.甲、乙两车从A地出发,沿同一路线驶向B地.甲车先出发匀速驶向B地,40min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地.甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:
①a=4.5;②甲的速度是60km/h;③乙出发80min追上甲;④乙刚到达货站时,甲距B地180km.其中正确的有( )组卷:2468引用:19难度:0.5 -
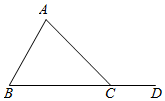 5.定理:三角形的一个外角等于与它不相邻的两个内角的和.
5.定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.
下列说法正确的是( )证法1:如图,
∵∠A+∠B+∠ACB=180°(三角形内角和定理),
又∵∠ACD+∠ACB=180°(平角定义),
∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换).
∴∠ACD=∠A+∠B(等式性质).证法2:如图,
∵∠A=76°,∠B=59°,
且∠ACD=135°(量角器测量所得)
又∵135°=76°+59°(计算所得)
∴∠ACD=∠A+∠B(等量代换).组卷:1368引用:23难度:0.7 -
 6.快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的距离y(km)与它们的行驶时间x(h)之间的函数关系.小欣同学结合图象得出如下结论:
6.快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的距离y(km)与它们的行驶时间x(h)之间的函数关系.小欣同学结合图象得出如下结论:
①快车途中停留了0.5h;
②快车速度比慢车速度多20km/h;
③图中a=340;
④快车先到达目的地.
其中正确的是( )组卷:3822引用:29难度:0.6 -
7.一次函数y=(a2+1)x-a的图象上有两点A(-1,y1),B(-2,y2),则y1与y2的大小关系为( )
组卷:721引用:4难度:0.7 -
8.小华和小刚兄弟两个同时从家去同一所学校上学,速度都是每分钟走50米.小华从家到学校走直线用了10分钟,而小刚从家出发先去找小明再到学校(均走直线),小刚到小明家用了6分钟,小明家到学校用了8分钟,小刚上学走了个( )
组卷:102引用:3难度:0.9
三、解答题(共8题,共62分)
-
24.已知E、F分别是AB、CD上的动点,P也为一动点.
(1)图(1)若AB∥CD,求证:∠P=∠BEP+∠PFD.
(2)图(2)若∠P=∠PFD-∠BEP,求证:AB∥CD.
(3)图(3)AB∥CD,移动E、F,使∠EPF=90°,作∠PEG=∠BEP,求的值.∠AEG∠PFD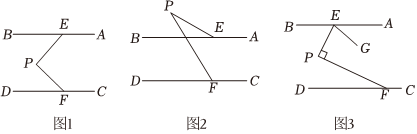 组卷:742引用:2难度:0.3
组卷:742引用:2难度:0.3 -
25.
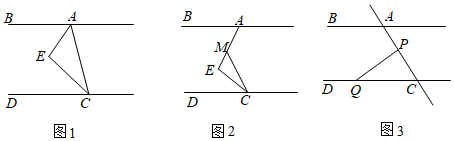
(1)特例发现:如图1,AB∥CD,CE平分∠ACD,AE平分∠BAC.请观察猜想∠AEC的度数并说明理由;
(2)类比探究:如图2,点M是AE上一点,当∠E=90°保持不变,移动直角顶点E,使CE平分∠MCD.∠BAE与∠MCD存在怎样的数量关系?并说明理由;
(3)拓展应用:如图3,P为线段AC上一定点,点Q为直线CD上一动点,点Q不与点C重合.∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论并说明理由.组卷:449引用:3难度:0.5


