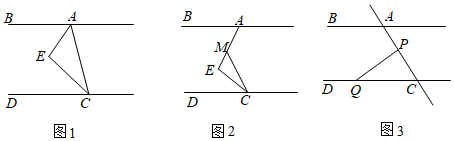
（1）特例发现：如图1，AB∥CD，CE平分∠ACD，AE平分∠BAC．请观察猜想∠AEC的度数并说明理由；
（2）类比探究：如图2，点M是AE上一点，当∠E=90°保持不变，移动直角顶点E，使CE平分∠MCD．∠BAE与∠MCD存在怎样的数量关系？并说明理由；
（3）拓展应用：如图3，P为线段AC上一定点，点Q为直线CD上一动点，点Q不与点C重合．∠CPQ+∠CQP与∠BAC有何数量关系？猜想结论并说明理由．
【考点】平行线的性质．
【答案】（1）∠AEC=90°；
（2）；
（3）∠BAC=∠PQC+∠QPC或∠PQC+∠QPC+∠BAC=180°．
（2）
∠
BAE
+
1
2
∠
MCD
=
90
°
（3）∠BAC=∠PQC+∠QPC或∠PQC+∠QPC+∠BAC=180°．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/26 4:0:8组卷：449引用：3难度：0.5
相似题
-
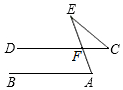1．如图，直线AB∥CD，∠A=70°，则∠EFC等于（ ）发布：2025/6/17 20:0:2组卷：261引用：1难度：0.8 -
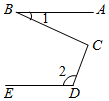2．如图，AB∥DE，那么∠BCD=（ ）发布：2025/6/17 20:30:2组卷：4000引用：7难度：0.5 -
3．已知：如图1，直线AB∥CD，EF分别交AB、CD于E、F两点，∠BEF、∠DFE的平分线相交于点K．
（1）求∠EKF的度数．（计算过程不准用三角形内角和）
（2）如图2，∠BEK、∠DFK的平分线相交于点K1，问∠K1与∠K的度数是否存在某种特定的等量关系？写出结论并证明．
（3）在图2中作∠BEK1、∠DFK1的平分线相交于点K2，作∠BEK2、∠DFK2的平分线相交于点K3，依此类推，作∠BEKn、∠DFKn的平分线相交于点Kn+1，请用含的n式子表示∠Kn+1的度数．（直接写出答案，不必写解答过程）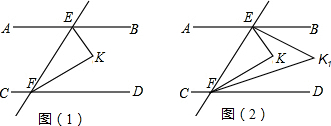
发布：2025/6/17 22:0:1组卷：518引用：6难度：0.3
