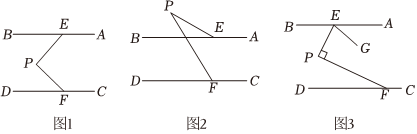
已知E、F分别是AB、CD上的动点，P也为一动点．
（1）图（1）若AB∥CD，求证：∠P=∠BEP+∠PFD．
（2）图（2）若∠P=∠PFD-∠BEP，求证：AB∥CD．
（3）图（3）AB∥CD，移动E、F，使∠EPF=90°，作∠PEG=∠BEP，求
∠
AEG
∠
PFD
的值．

【答案】见试题解答内容

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/8/26 4:0:8组卷：742引用：2难度：0.3

相似题

1．（1）如图1，AC平分∠DAB，∠1=∠2，试说明AB与CD的位置关系，并予以证明；
（2）如图2，AB∥CD，AB的下方两点E，F满足：BF平分∠ABE，DF平分∠CDE，若∠DFB=20°，∠CDE=70°，求∠ABE的度数
（3）在前面的条件下，若P是BE上一点；G是CD上任一点，PQ平分∠BPG，PQ∥GN，GM平分∠DGP，下列结论：①∠DGP-∠MGN的值不变；②∠MGN的度数不变．可以证明，只有一个是正确的，请你作出正确的选择并求值．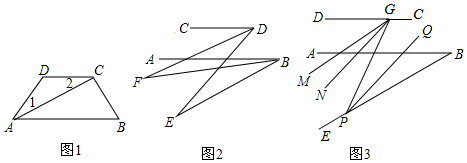
发布：2025/6/17 22:0:1组卷：1366引用：7难度：0.5
解析
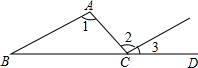2．如图，已知∠1=∠2，∠3=30°，则∠B的度数是（　　）
A．20° B．30° C．40° D．60°
发布：2025/6/17 22:0:1组卷：951引用：20难度：0.9
解析
3．已知：如图，AE⊥BC，FG⊥BC，∠1=∠2，求证：AB∥CD．
发布：2025/6/17 16:0:1组卷：2647引用：42难度：0.5
解析

已知E、F分别是AB、CD上的动点，P也为一动点．（1）图（1）若AB∥CD，求证：∠P=∠BEP+∠PFD．（2）图（2）若∠P=∠PFD-∠BEP，求证：AB∥CD．（3）图（3）AB∥CD，移动E、F，使∠EPF=90°，作∠PEG=∠BEP，求∠AEG∠PFD的值．