2022-2023学年湖南省湖湘教育三新探索协作体高一（下）期中数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知A={x|（2-x）（x+3）＞4}，B={x|log₂x＜1}，则A∩B=（　　）

  A．（-2，1）

  B．（0，2）

  C．（-3，2）

  D．（0，1）
  组卷：35引用：1难度：0.8

  解析

• 2．已知i为虚数单位，复数z=（3-i³）（1+ai）为纯虚数，则|z|=（　　）

  A．0

  B． - 1 3

  C．3

  D．10
  组卷：69引用：3难度：0.9

  解析

• 3．已知正三棱锥ABCD，各棱长均为

  3

  ，则其外接球的体积为（　　）

  A． 9 3 8 π

  B． 81 2 16 π

  C． 9 2 8 π

  D． 9 3 16 π
  组卷：319引用：4难度：0.6

  解析

• 4．若“x²+3x-4＜0”是“x²-（3m+3）x+2m²+3m＞0”的一个充分不必要条件，则实数m的取值范围是（　　）

  A．m≤-4或m≥1

  B．m≤-4或m＞-3

  C．m≤-1或m≥4

  D．m＜-3或m≥4
  组卷：165引用：1难度：0.8

  解析

• 5．在△ABC中，

  2

  BD

  =

  BC

  ，

  3

  BE

  =

  BA

  ，且CE与AD交于点P，若

  CP

  =

  x

  CA

  +

  y

  CB

  （x,y∈R），则x+y=（　　）

  A． 2 5

  B． 3 5

  C． 4 5

  D．1
  组卷：169引用：5难度：0.7

  解析

• 6．已知正实数a,b满足a+2b=4，则

  1

  a

  +

  1

  b

  +

  1

  的最小值是（　　）

  A．1

  B． 33 28

  C． 3 + 2 2 6

  D． 1 + 3 3
  组卷：1155引用：4难度：0.8

  解析

• 7．将函数

  f

  （

  x

  ）

  =

  sin

  （

  2

  x

  -

  π

  6

  ）

  +

  cos

  2

  x

  -

  sin

  2

  x

  的图象向左平移

  φ

  （

  0

  ＜

  φ

  ＜

  π

  2

  ）

  个单位长度后得到函数g（x）的图象．若函数g（x）的图象关于直线

  x

  =

  π

  3

  轴对称，则φ的值为（　　）

  A． 5 π 12

  B． π 3

  C． π 4

  D． π 6
  组卷：61引用：1难度：0.8

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

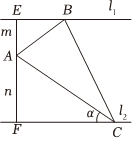• 21．如图，直线l₁∥l₂，点A是l₁，l₂之间的一个定点，过点A的直线EF垂直于直线l₁，AE=m,AF=n（m,n为常数），点B，C分别为l₁，l₂上的动点，已知

  ∠

  BAC

  =

  π

  4

  ．设

  ∠

  ACF

  =

  α

  （

  0

  ＜

  α

  ＜

  π

  4

  ）

  ，△ABC的面积为S（α）．
  （1）写出S（α）的解析式；
  （2）求S（α）的最小值．
  组卷：21引用：1难度：0.5

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  lg

  1

  -

  x

  1

  +

  x

  ．
  （1）证明：函数f（x）为奇函数；
  （2）判断函数f（x）的单调性；
  （3）若函数

  h

  （

  x

  ）

  =

  f （ x ） ，- 1 ＜ x ＜ 1

  k x 2 + 1 ， x ≤ - 1 或 x ≥ 1

  ，其中k≤0，讨论函数y=h（h（x））-2的零点个数．
  组卷：115引用：2难度：0.5

  解析