2022-2023学年辽宁省沈阳市郊联体高一（下）期中数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个是符合题目要求的.

• 1．cos20°cos385°-cos70°sin155°=（　　）

  A． 1 2

  B． 2 2

  C． 3 2

  D．1
  组卷：154引用：2难度：0.8

  解析

• 2．下列四个函数中，以π为最小正周期，且在区间

  （

  π

  2

  ，

  π

  ）

  上为减函数的是（　　）

  A．y=2|sinx|

  B．y=cosx

  C．y=sin2x

  D．y=|cosx|
  组卷：986引用：6难度：0.9

  解析

• 3．已知

  |

  a

  |

  =

  1

  ，

  |

  b

  |

  =

  2

  ，且

  a

  ⊥

  （

  a

  +

  b

  ）

  则

  a

  在

  b

  上的投影数量为（　　）

  A．1

  B．-1

  C． 1 2

  D． - 1 2
  组卷：119引用：2难度：0.8

  解析

• 4．古希腊的数学家毕达哥拉斯通过研究正五边形和正十边形的作图，发现了黄金分割率φ，且黄金分割率的值也可以用2sin18°表示，则

  8

  φ

  2

  cos

  2

  18

  °

  2

  -

  φ

  =（　　）

  A．1

  B．2

  C．4

  D．8
  组卷：136引用：2难度：0.7

  解析

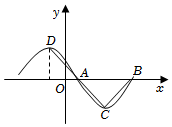• 5．已知f（x）=sin（ωx-

  π

  6

  ）-cosωx（ω＞0），将f（x）图象上横坐标伸长为原来的2倍（纵坐标不变时），得到求g（x）的图象．g（x）的部分图象如图所示（D，C分别是函数的最高点和最低点），其中

  CA

  •

  CB

  =

  |

  AD

  |

  2

  2

  ，则ω=（　　）

  A． π 4

  B． π 2

  C．π

  D．2π
  组卷：210引用：2难度：0.5

  解析

• 6．已知

  a

  =

  （

  cos

  （

  α

  -

  π

  6

  ）

  ，

  1

  2

  ）

  ，

  b

  =

  （

  1

  ，-

  2

  sinα

  ）

  且

  a

  •

  b

  =

  1

  3

  ，则

  sin

  （

  π

  6

  -

  2

  α

  ）

  =（　　）

  A． 7 9

  B． - 7 9

  C． ± 7 9

  D． - 2 9
  组卷：82引用：1难度：0.6

  解析

• 7．已知函数f（x）=

  3

  sin²ωx+2sinωxcosωx-

  3

  cos²ωx-1（ω＞0），给出下列4个结论：
  ①f（x）的最小值是-3；
  ②若ω=1，则f（x）在区间

  （

  -

  π

  12

  ，

  5

  π

  12

  ）

  上单调递增；
  ③将y=sinx的函数图象横坐标缩短为原来的

  1

  4

  倍，再向右平移

  π

  12

  个单位长度，再向下平移1个单位长度，可得函数y=f（x）的图象，则ω=2；
  ④若存在互不相同的x₁，x₂，x₃∈[0，π]，使得f（x₁）+f（x₂）+f（x₃）=3，则ω≥

  29

  12

  
  其中所有正确结论的序号是（　　）

  A．①②④

  B．①③④

  C．②③④

  D．①②
  组卷：192引用：3难度：0.5

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

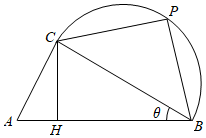• 21．某公司欲生产一款迎春工艺品回馈消费者，工艺品的平面设计如图所示，该工艺品由直角△ABC和以BC为直径的半圆拼接而成，点P为半圈上一点（异于B，C），点H在线段AB上，且满足CH⊥AB．已知∠ACB=90°，AB=1dm,设∠ABC=θ．
  （1）为了使工艺礼品达到最佳观赏效果，需满足∠ABC=∠PCB，且CA+CP达到最大．当θ为何值时，工艺礼品达到最佳观赏效果；
  （2）为了工艺礼品达到最佳稳定性便于收藏，需满足∠PBA=60°，且CH+CP达到最大．当θ为何值时，CH+CP取得最大值，并求该最大值．
  组卷：326引用：22难度：0.5

  解析

• 22．已知O为坐标原点，对于函数f（x）=asinx+bcosx,称向量

  OM

  =（a,b）为函数f（x）的伴随向量，同时称函数f（x）为向量

  OM

  的伴随函数．
  （Ⅰ）设函数g（x）=

  3

  sin

  （

  x

  -

  π

  ）

  -

  sin

  （

  3

  2

  π

  -

  x

  ）

  ，试求g（x）的伴随向量

  OM

  ；
  （Ⅱ）记向量

  ON

  =（1，

  3

  ）的伴随函数为f（x），求当f（x）=

  8

  5

  且

  x

  ∈

  （

  -

  π

  3

  ，

  π

  6

  ）

  时cosx的值；
  （Ⅲ）由（Ⅰ）中函数g（x）的图象（纵坐标不变）横坐标伸长为原来的2倍，再把整个图象向右平移

  2

  π

  3

  个单位长度得到h（x）的图象，已知A（-2，3），B（2，6），问在y=h（x）的图象上是否存在一点P，使得

  AP

  ⊥

  BP

  ．若存在，求出P点坐标；若不存在，说明理由．
  组卷：184引用：4难度：0.3

  解析