2023-2024学年广东省云浮市罗定中学城东学校高二（上）月考数学试卷（二）

一、单选题（每小题5分，共40分.每个小题仅有一个答案是正确的）

• 1．已知空间向量

  a

  =

  （

  0

  ，

  1

  ，

  2

  ）

  ，

  b

  =

  （

  -

  1

  ，

  2

  ，

  2

  ）

  ，则向量

  a

  在向量

  b

  上的投影向量是（　　）

  A． （ - 1 3 ， 2 3 ， 2 3 ）	B． （ - 2 3 ， 4 3 ， 4 3 ）
  C．（-2，4，4）	D． （ - 4 3 ， 2 3 ， 2 3 ）
  组卷：877引用：22难度：0.8

  解析

• 2．若直线x-2y-3=0与mx+3y-6=0互相垂直，则m=（　　）

  A． - 3 2

  B．6

  C． 3 2

  D．-6
  组卷：74引用：3难度：0.9

  解析

• 3．直线kx-y+1=3k,当k变动时，所有直线都通过定点（　　）

  A．（0，0）

  B．（0，1）

  C．（3，1）

  D．（2，1）
  组卷：145引用：8难度：0.8

  解析

• 4．设点A（3，-3），B（-2，-2），直线l过点P（1，1）且与线段AB相交，则l的斜率k的取值范围是（　　）

  A．k≥1或k≤-4

  B．k≥1或k≤-2

  C．-4≤k≤1

  D．-2≤k≤1
  组卷：375引用：14难度：0.8

  解析

• 5．已知直线x-2y+t=0经过点（2，-1），则该直线在y轴上的截距为（　　）

  A． 1 2

  B．- 1 2

  C．2

  D．-2
  组卷：127引用：3难度：0.7

  解析

• 6．在三棱柱ABC-A₁B₁C中，M，N分别为A₁C₁，B₁B的中点，若

  MN

  =

  x

  AB

  +

  y

  AC

  +

  z

  A

  A

  1

  ，则（x,y,z）=（　　）

  A．（1，- 1 2 ，- 1 2 ）	B．（1， 1 2 ，- 1 2 ）
  C．（-1， 1 2 ， 1 2 ）	D．（-1， 1 2 ，- 1 2 ）
  组卷：279引用：5难度：0.8

  解析

• 7．在正方体ABCD-A₁B₁C₁D₁中，直线BB₁与平面ACD₁所成角的余弦值为（　　）

  A． 6 3

  B． 3 3

  C． 2 3

  D． 2 3
  组卷：217引用：6难度：0.5

  解析

四、解答题（本大题共6小题，共70分，解答时应写出文字说明、证明过程或演算步骤）

• 21．已知直线l：ax-y+2-a=0恒过点P，且与x轴，y轴分别交于A，B两点，O为坐标原点．
  （1）求点P的坐标；
  （2）当点O到直线l的距离最大时，求直线l的方程；
  （3）当|PA|•|PB|取得最小值时，求△AOB的面积．
  组卷：395引用：9难度：0.7

  解析

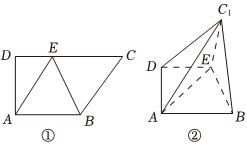• 22．图①是直角梯形ABCD，AB∥CD，∠D=90°，四边形ABCE是边长为2的菱形，并且∠BCE=60°，以BE为折痕将△BCE折起，使点C到达C₁的位置，且AC₁=

  6

  ．
  （1）求证：平面BC₁E⊥平面ABED；
  （2）在棱DC₁上是否存在点P，使得点P到平面ABC₁的距离为

  15

  5

  ？若存在，求出直线EP与平面ABC₁所成角的正弦值；若不存在，请说明理由．
  组卷：508引用：18难度：0.6

  解析