2023-2024学年北京市101中学高三（上）统练数学试卷（五）

一、选择题共10小题。在每小题列出的四个选项中，选出符合题目要求的一项。

• 1．已知集合P={x|-1≤x≤1}，

  Q

  =

  {

  x

  ∈

  N

  |

  x

  x

  -

  2

  ≤

  0

  }

  ，则P∩Q=（　　）

  A．{x|0≤x≤1}

  B．{x|-1≤x≤0}

  C．{0，1，2}

  D．{0，1}
  组卷：29引用：2难度：0.7

  解析

• 2．等差数列{a_n}中，a₂=3，a₃+a₄=9则a₁a₆的值为（　　）

  A．14

  B．18

  C．21

  D．27
  组卷：156引用：17难度：0.9

  解析

• 3．在△ABC中，角A、B、C所对的边分别为a、b、c,已知a=3，b=

  6

  ，A=

  π

  3

  ，则角B等于（　　）

  A． π 4

  B． 3 π 4

  C． π 4 或 3 π 4

  D．以上都不对
  组卷：89引用：9难度：0.9

  解析

• 4．将y=2cos（

  x

  3

  +

  π

  6

  ）的图象通过平移变换，得到一个奇函数的图象，则这个变换可以是（　　）

  A．左移 π 3 个单位	B．右移 π 3 个单位
  C．左移π个单位	D．右移π个单位
  组卷：140引用：4难度：0.9

  解析

• 5．在△ABC中，“A＞30°”是“sinA＞

  1

  2

  ”的（　　）

  A．充分而不必要条件	B．必要而不充分条件
  C．充分必要条件	D．既不充分也必要条件
  组卷：329引用：45难度：0.9

  解析

• 6．在下列函数中，最小值是2的是（　　）

  A．y= x 2 + 2 x

  B．y= x + 2 x + 1 （x＞0）

  C．y=sinx+ 1 sinx ，x∈（0， π 2 ）

  D．y=7x+7-x
  组卷：190引用：5难度：0.9

  解析

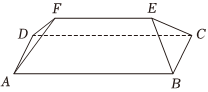• 7．坡屋顶是我国传统建筑造型之一，蕴含着丰富的数学元素．安装灯带可以勾勒出建筑轮廓，展现造型之美．如图，某坡屋顶可视为一个五面体，其中两个面是全等的等腰梯形，两个面是全等的等腰三角形．若AB=25m,BC=AD=10m,且等腰梯形所在的平面、等腰三角形所在的平面与平面ABCD的夹角的正切值均为

  14

  5

  ，则该五面体的所有棱长之和为（　　）

  A．102m

  B．112m

  C．117m

  D．125m
  组卷：293引用：7难度：0.4

  解析

三、解答题共6小题。解答应写出文字说明、演算步骤或证明过程。

• 20．已知函数f（x）=e^ax（x-1）²．
  （1）若a=1，求f（x）在（0，f（0））处切线方程；
  （2）求f（x）的极大值与极小值；
  （3）证明：存在实数M，当a＞0时，函数y=f（x）-M有三个零点．
  组卷：447引用：7难度：0.5

  解析

• 21．对于一个n行n列的数表A_n×n（n≥2），用a_i,j表示数表中第i行第j列的数，其中a_i,j∈Z（i,j=1，2，⋯，n），且数表A_n×n满足以下两个条件：
  ①

  n

  ∑

  j

  =

  1

  a

  1

  ，

  j

  =

  n

  ；
  ②a_i+1，j+1=a_i,j，规定a_i+1，n+1=a_i+1，1（i=1，2，⋯，n-1，j=1，2，⋯，n）．
  （Ⅰ）已知数表A_3×3中，a_1，1=3，a_1，2=-1．写出a_1，3，a_2，2，a_3，1的值；
  （Ⅱ）若a_1，1+⋯+a_1，k-k=max{a_1，1-1，a_1，1+a_1，2-2，⋯，a_1，1+⋯+a_1，n-n}（k∈{1，2，⋯，n}），其中maxM表示数集M中最大的数．规定a_1，n+1=a_1，1．证明：a_1，k+1-1≤0；
  （Ⅲ）证明：存在m∈{1，2，⋯，n}，对于任意l∈{1，2，⋯，n}，有a_m,1+a_m,2+⋯+a_m,l≤l.
  组卷：112引用：5难度：0.1

  解析