2022-2023学年北京市首都师大附中高一(下)期中数学试卷
发布:2024/6/24 8:0:9
一、选择题(本大题共10小题,每小题4分,共40分.在每小题所列出的四个选项中,只有一项是最符合题目要求的)
-
1.已知向量
=(1,m),a=(-1,1),b=(3,0),若c∥(a+b),则m=( )c组卷:334引用:7难度:0.8 -
2.若角α的终边在第三象限,则下列三角函数值中小于零的是( )
组卷:683引用:5难度:0.8 -
3.下列选项使得函数
单调递减的是( )f(x)=sin(2x-π3)组卷:297引用:2难度:0.7 -
4.在△ABC中,AB=1,AC=
,2,则∠B=( )∠C=π6组卷:403引用:4难度:0.9 -
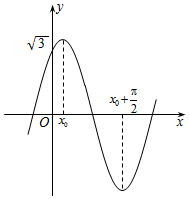 5.已知函数的图象如图所示,则函数f(x)的解析式的值为( )f(x)=2sin(ωx+φ)(ω>0,|φ|<π2)组卷:136引用:6难度:0.7
5.已知函数的图象如图所示,则函数f(x)的解析式的值为( )f(x)=2sin(ωx+φ)(ω>0,|φ|<π2)组卷:136引用:6难度:0.7 -
6.已知α∈(-π,π),且sinα=-cos
,则α=( )π7组卷:138引用:4难度:0.7 -
7.已知向量a,b是两个单位向量,则“<a,b>为锐角”是“
”的( )|a-b|<2组卷:416引用:12难度:0.7
三、解答题(本大题共5小题,共50分.应写出文字说明,证明过程或演算步骤)
-
20.设函数
(ω>0,m∈R).在下列条件①、条件②、条件③这三个条件中选择两个作为已知,使得f(x)存在.f(x)=4sinωx2cos(ωx2-π3)+m
条件①:f(-x)=f(x);
条件②:f(x)的最小正周期为π;
条件③:f(x)的最大值与最小值之和为0.
(1)求函数f(x)的解析式;
(2)若函数f(x)在区间[0,a]上是增函数,求实数a的最大值.
注:如果选择的条件不符合要求,得0分;如果选择多组条件分别解答,按第一组解答计分.组卷:104引用:2难度:0.5 -
21.对平面向量
,定义α=(x,y).M(α)=|x|+|y|
(1)设,求α=(3,-2);M(α)
(2)设A(0,2),B(2,0),C(4,1),D(5,3),E(6,2),点P(x,y)是平面内的动点,其中x,y是整数.
(ⅰ)记,M(PA),M(PB),M(PC),M(PD)的最大值为t(P),直接写出t(P)的最小值及当t(P)取最小值时,点P的坐标.M(PE)
(ⅱ)记.求s(P)的最小值及相应的点P的坐标.s(P)=M(PA)+M(PB)+M(PC)+M(PD)+M(PE)组卷:163引用:2难度:0.3


