2022-2023学年湖南省永州市零陵区八年级（下）期末数学试卷
发布：2024/7/1 8:0:9
一、选择题（共10个小题，每小题3分，共30分，请将正确选项填涂到答题卡上）
-
1．下列文字中是中心对称图形的是（ ）
组卷：16引用：2难度：0.9 -
2．如图是某校门口的电动伸缩门，电动伸缩门利用了（ ）性质组卷：266引用：6难度：0.7 -
3．若正比例函数y=kx（k≠0）的函数值y随x的增大而减少，则一次函数y=2x-k的图象大致是（ ）
组卷：358引用：2难度：0.7 -
4．如图，在Rt△ABC中，∠ABC=90°，点D是AC边上的中点，∠ADB=120°，则∠C=（ ）组卷：109引用：3难度：0.7 -
5．如图，小明与小亮在玩“五子棋”，小明是黑子，他把第四子下在棋盘坐标的（1，-2）上，则小亮下的白色第三子的棋盘坐标是（ ）组卷：75引用：3难度：0.5 -
6．勾股定理现约有500多种证明方法，是数学定理中证明方法最多的定理之一，在中国周朝的商定提出了“勾三股四弦五”的勾股定理的特例，古埃及人用“结绳法”在金字塔等建筑的拐角处作出直角；“普林顿322”的古巴比伦泥板上记载了很多勾股数；公元前6世纪古希腊的毕达哥拉斯学派用演绎法证明了勾股定理．下面图例中，不能证明勾股定理的是（ ）
组卷：63引用：5难度：0.7 -
7．下列关系中，属于成正比例函数关系的是（ ）
组卷：402引用：2难度：0.7 -
8．如图，正方形ABCD的边长为4，建立平面直角坐标系后，表示点D的坐标正确的是（ ）
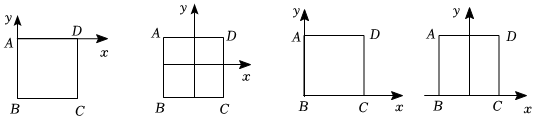组卷：33引用：3难度：0.5
三、解答题（本大题共9个小题，共72分，解答题要求写出证明步骤或解答过程）
-
24．定义共弦、共弦角如下：
共弦：将正多边形绕某顶点顺时针旋转60°得到的新正多边形与原正多边形相交于一点O，连接旋转中心与交点O，把这条线段叫做正多边形的共弦：图1以正四边形为例，图2以正五边形为例，线段OA即为正四（五）边形的共弦．共弦角：共弦与离原正多边形最近的边组成的角叫做共弦角：如图1，∠OAB是共弦角，因此0°＜∠OAB＜90°．
（1）如图1，四边形ABCD是正方形．求证：∠OAB=∠OAD'，并求出∠OAB的值；
（2）依照（1）的方法，有人求出了以下正多边形的共弦角：
正五边形：12（108°-60°）=24°
正六边形：12（120°-60°）=30°
正七边形：12（57×180°-60°）
请你根据以上结论，猜想任意正n边形的共弦角的度数（用含n的代数式表示）？并写出这样猜想的理由．
（3）请审视以上数学问题、问题解决以及猜想过程，提出至少两个与之有关的、你认为需要进一步探究的数学问题．
组卷：52引用：4难度：0.5 -
25．如图，在平面直角坐标系中，直线AC：y=x-1与x轴相交于点A，将直线AC绕点A逆时针旋转90°得到直线AB：y=-2x+b,直线AB与y轴相交于点B，在直线AC上截取AC，使AC=AB，过B、C两点的直线BC交x轴于点D．12
（1）点A的坐标为 ，点C的坐标为 ；
（2）若点E是线段BC上的动点，△ABE的面积为5时，求点E的坐标；
（3）在符合以上条件的A、B、E三点的基础上，平面内是否存在一点F，使得以点A、B、E、F为顶点的四边形是平行四边形，若存在，直接写出点F的可能坐标（至少写两个）；若不存在，请说明理由．组卷：144引用：4难度：0.3
