定义共弦、共弦角如下：
共弦：将正多边形绕某顶点顺时针旋转60°得到的新正多边形与原正多边形相交于一点O，连接旋转中心与交点O，把这条线段叫做正多边形的共弦：图1以正四边形为例，图2以正五边形为例，线段OA即为正四（五）边形的共弦．共弦角：共弦与离原正多边形最近的边组成的角叫做共弦角：如图1，∠OAB是共弦角，因此0°＜∠OAB＜90°．
（1）如图1，四边形ABCD是正方形．求证：∠OAB=∠OAD'，并求出∠OAB的值；
（2）依照（1）的方法，有人求出了以下正多边形的共弦角：
正五边形：12（108°-60°）=24°
正六边形：12（120°-60°）=30°
正七边形：12（57×180°-60°）
请你根据以上结论，猜想任意正n边形的共弦角的度数（用含n的代数式表示）？并写出这样猜想的理由．
（3）请审视以上数学问题、问题解决以及猜想过程，提出至少两个与之有关的、你认为需要进一步探究的数学问题．
1
2
（
108
°
-
60
°
）
=
24
°
1
2
（
120
°
-
60
°
）
=
30
°
1
2
（
5
7
×
180
°
-
60
°
）
【考点】四边形综合题．
【答案】（1）∠OAB的度数为：15°；
（2）正n边形的共弦角的度数[-60°]或60°-；
（3）见解析
（2）正n边形的共弦角的度数
1
2
（
n
-
2
）
×
180
°
n
180
°
n
（3）见解析
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/12 8:0:9组卷：52引用：4难度：0.5
相似题
-
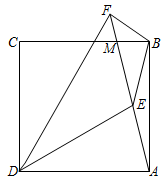1．如图，点M是正方形ABCD的边BC上一点，连接AM，点E是线段AM上一点，∠CDE的平分线DF交AM的延长线于点F，连接BE．
（1）若点E是线段AM的中点，且CM=2BM，BE=10，求正方形ABCD的面积；
（2）若DA=DE，求证：BF+DF=AF．2发布：2025/6/20 7:0:1组卷：331引用：2难度：0.1 -
2．如图所示，在▱ABCD中，连接对角线AC．把AB绕着点A逆时针旋转60°，得到线段AE，点E在边BC上．点F在线段AE上，且AF=CE．连接BF，DF，G是BF的中点，连接AG，CG．
（1）求证：∠BAG=∠EAC；
（2）猜想AG与CG存在的数量关系，并证明你猜想的结论；
（3）当∠BAG=15°时，请直接写出DF与AB存在的数量关系．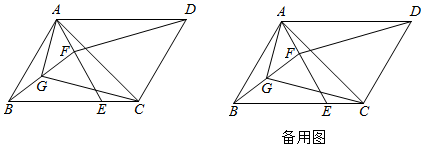
发布：2025/6/20 7:0:1组卷：290引用：3难度：0.1 -
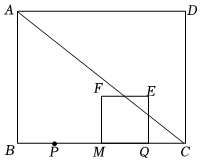3．如图，在矩形ABCD中，BC=8，tan∠BAC=．点P从点B出发，沿BC以每秒2个单位长度的速度向终点C运动，已知边BC的中点是点M，点P关于点M的对称点为点Q．当点P不与点M重合时，以MQ为边在BC的上方作正方形MQEF，连结AC，设点P的运动时间为t秒．43
（1）线段AB的长为 ．
（2）用含t的代数式表示线段MQ的长．
（3）当点F恰好落在线段AC上时，求t的值．
（4）当正方形MQEF与△ACD重叠部分的图形是三角形时，直接写出t的取值范围．发布：2025/6/20 8:0:2组卷：90引用：2难度：0.1
