2023年湖南省衡阳市中考数学模拟试卷
发布:2024/5/12 8:0:9
一、选择题(本大题共12小题,每小题3分,共36分,每小题给出的四个选项中,只有一项符合题目要求)
-
1.在0、
、-1、13这四个数中,最小的数是( )2组卷:444引用:10难度:0.9 -
2.下列北京冬奥会运动标识图案是轴对称图形的是( )
组卷:772引用:14难度:0.9 -
3.某村通过直播带货对产出的稻虾米进行线上销售,连续7天的销量(单位:袋)分别为:105,103,105,110,108,105,108,这组数据的众数和中位数分别是( )
组卷:243引用:2难度:0.7 -
 4.某个立体图形的侧面展开图如图所示,它的底面是正三角形,那么这个立体图形是( )组卷:461引用:4难度:0.7
4.某个立体图形的侧面展开图如图所示,它的底面是正三角形,那么这个立体图形是( )组卷:461引用:4难度:0.7 -
5.下列计算正确的是( )
组卷:45引用:4难度:0.7 -
6.不等式组
的解集在数轴上可表示为( )3-x≤512(x+1)<1组卷:148引用:5难度:0.9 -
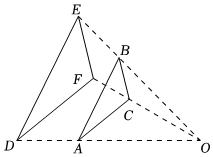 7.如图,△ABC与△DEF位似,点O为位似中心,相似比为2:3.若△ABC的周长为4,则△DEF的周长是( )组卷:1755引用:19难度:0.7
7.如图,△ABC与△DEF位似,点O为位似中心,相似比为2:3.若△ABC的周长为4,则△DEF的周长是( )组卷:1755引用:19难度:0.7 -
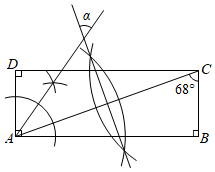 8.如图,依据尺规作图的痕迹,计算∠α的度数为( )组卷:1262引用:11难度:0.7
8.如图,依据尺规作图的痕迹,计算∠α的度数为( )组卷:1262引用:11难度:0.7
三、解答题(本大题共8个小题,共66分,解答应写出文字说明、证明过程或演算步骤)
-
25.如图,四边形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=CD=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.当其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ,设运动时间为t秒(0<t<4).
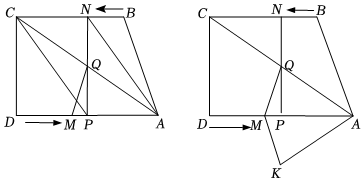
(1)连接AN、CP,BN=,DM=,(用含t的代数式表达),当t=时,四边形ANCP为平行四边形;
(2)将△AQM沿AD翻折,得到△AKM.在运动过程中,是否存在某时刻t,使四边形AQMK为菱形,若存在,求出t的值;若不存在,请说明理由.
(3)设四边形DMQC的面积为y,求y与t的函数关系式;是否存在某一时刻t,使四边形DMQC的面积与△ABC的面积相等?若存在,求出t的值;若不存在,请说明理由;组卷:58引用:1难度:0.1 -
26.如图,B(2m,0)、C(3m,0)是平面直角坐标系中两点,其中m为常数,且m>0,E(0,n)为y轴上一动点,以BC为边在x轴上方作矩形ABCD,使AB=2BC,画射线OA,把△ADC绕点C逆时针旋转90°得△A′D′C′,连接ED′,抛物线y=ax2+bx+n(a≠0)过E、A′两点.
(1)填空:∠AOB=°,用m表示点A′的坐标:A′;
(2)当抛物线的顶点为A′,抛物线与线段AB交于点P,且时,△D′OE与△ABC是否相似?说明理由;BPAP=13
(3)若E与原点O重合,抛物线与射线OA的另一个交点为M,过M作MN垂直y轴,垂足为N.
①求a、b、m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为5,请你探究a的取值范围.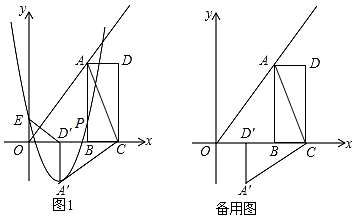 组卷:393引用:3难度:0.6
组卷:393引用:3难度:0.6


