2023年湖北省襄阳五中高考数学适应性试卷（一）
发布：2024/8/11 0:0:1
一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
-
1．设复数X，则在复平面内
对应的点位于（ ）z+1z组卷：26引用：2难度：0.8 -
2．函数
的图象大致为（ ）f（x）=ex-1ex+1•cosx组卷：104引用：3难度：0.8 -
3．已知
，则α∈（0，π2），sin4α1+cos4α=sinαcosα-2=（ ）tanα2组卷：412引用：5难度：0.7 -
4．希伯特在1990年提出了孪生素数猜想：在自然数集中，孪生素数对有无穷多个，其中孪生素数是指相差2的素数对，即若p和p+2均是素数，素数对（p,p+2）称为孪生素数，从16以内的素数中任意取两个，其中能构成孪生素数的概率为（ ）
组卷：66引用：3难度：0.6 -
5．希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名．他发现：“平面内到两个定点A，B的距离之比为定值λ（λ≠1）的点的轨迹是圆”．后来，人们将这个圆以他的名字命名，称为阿波罗尼斯圆，简称阿氏圆．已知在平面直角坐标系xOy中，A（-4，1），B（-4，4），若点P是满足
的阿氏圆上的任意一点，点Q为抛物线C：y2=16x上的动点，Q在直线x=-4上的射影为R，则|PB|+2|PQ|+2|QR|的最小值为（ ）λ=12组卷：221引用：3难度：0.5 -
6．图1中，正方体ABCD-EFGH的每条棱与正八面体MPORSN（八个面均为正三角形）的一条棱垂直且互相平分．将该正方体的顶点与正八面体的顶点连结，得到图2的十二面体，该十二面体能独立密铺三维空间．若AB=1，则点M到直线RG的距离等于（ ）
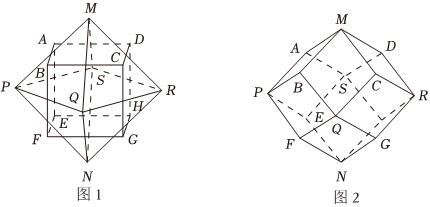组卷：83引用：4难度：0.6 -
7．在△ABC中，已知
，AC=3BC，sin∠BDC=3sin∠BAC，当AD=2DC取得最小值时，△ABC的面积为（ ）CA•CB-|AB|组卷：468引用：3难度：0.5
四、解答题：（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）
-
21．已知离心率为
的椭圆22的左焦点为F，左、右顶点分别为A1、A2，上顶点为B，且△A1BF的外接圆半径大小为C：x2a2+y2b2=1（a＞b＞0）．3
（1）求椭圆C方程；
（2）设斜率存在的直线l交椭圆C于P，Q两点（P，Q位于x轴的两侧），记直线A1P、A2P、A2Q、A1Q的斜率分别为k1、k2、k3、k4，若，求△A2PQ面积的取值范围．k1+k4=53（k2+k3）组卷：187引用：6难度：0.5 -
22．如果曲线y=f（x）存在相互垂直的两条切线，称函数y=f（x）是“正交函数”．已知f（x）=x2+ax+2lnx,设曲线y=f（x）在点M（x0，f（x0））处的切线为l1．
（1）当f'（1）=0时，求实数a的值；
（2）当a=-8，x0=8时，是否存在直线l2满足l1⊥l2，且l2与曲线y=f（x）相切？请说明理由；
（3）当a≥-5时，如果函数y=f（x）是“正交函数”，求满足要求的实数a的集合D；若对任意a∈D，曲线y=f（x）都不存在与l1垂直的切线l2，求x0的取值范围．组卷：334引用：4难度：0.3
