2023年吉林省长春市二道区赫行实验学校中考数学质检试卷（5月份）

一、选择题（本大题共8小题，每小题3分，共24分）

• 1．在实数-3、-2、0、2中，最小的实数是（　　）

  A．-3

  B．-2

  C．0

  D．2
  组卷：269引用：6难度：0.9

  解析

• 2．2023年春节期贺岁片《满江红》火爆出圈，据电影统计消息，截止2月2日10：00，上映仅14天，电影票房便已突破35.8亿元，将数据35.8亿用科学记数法可表示为（　　）

  A．35.8×108

  B．0.358×1010

  C．3.58×109

  D．3.58×1010
  组卷：75引用：3难度：0.9

  解析

• 3．如图是一个由5个相同的正方体组成的立体图形，它的左视图是（　　）

  A．

  B．

  C．

  D．
  组卷：123引用：2难度：0.8

  解析

• 4．不等式-2x+4≥0的解集在数轴上表示正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：60引用：1难度：0.5

  解析

• 5．某批电子产品进价为200元/件，售价为350元/件，为提高销量，商店准备将这批电子产品降价出售，若要保证单件利润率不低于5%，则该批电子产品最多可降价多少元？若设该批电子产品可降价x元，则可列不等式为（　　）

  A． 350 - 200 - x 200 ≥ 5 %	B． 350 - 200 - x 200 ≤ 5 %
  C． 350 - 200 - x 350 ≥ 5 %	D． 350 - 200 - x 350 ≤ 5 %
  组卷：194引用：1难度：0.8

  解析

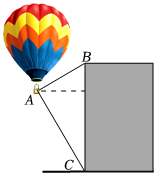• 6．如图所示，热气球的探测器显示，从热气球A处看一栋楼顶部B处的仰角为α，看这栋楼底部C处的俯角为β，热气球A处与楼的水平距离为120m,则这栋楼的高度为（　　）

  A．120（tanα+tanβ）m	B．120（tanα-tanβ）m
  C．120（sinα+sinβ）m	D．120（sinα+tanβ）m
  组卷：441引用：4难度：0.5

  解析

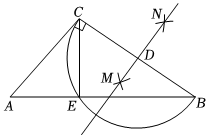• 7．如图，在△ABC中，∠ACB=90°，AC=5，BC=12，按以下步骤作图：①分别以B、C为圆心，大于

  1

  2

  BC

  的长为半径画圆弧，两弧相交于点M和点N；②作直线MN，交BC于点D；③以点D为圆心，DC的长为半径画圆弧，交AB于点E，连结CE，则AE的长为（　　）

  A． 144 13

  B． 25 12

  C． 25 13

  D． 60 13
  组卷：71引用：1难度：0.5

  解析

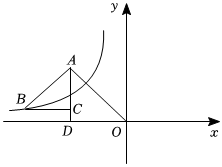• 8．如图，△OAD和△BAC都是等腰直角三角形，∠ADO=∠ACB=90°，反比例函数

  y

  =

  k

  x

  在第二象限的图象经过点B，且OA²-AB²=12，则k的值是（　　）

  A．-6

  B．-4

  C．4

  D．6
  组卷：234引用：1难度：0.5

  解析

三、解答题（本大题共10小题，共78分）

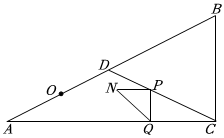• 23．如图，在△ABC中，∠ACB=90°，BC=2，AC=4，CD是边AB的中线．动点P从点C出发，以每秒

  5

  个单位长度的速度沿折线CD-DB向终点B运动．过点P作PQ⊥AC于点Q，以PQ为边作等腰直角三角形PQN，∠QPN=90°，使点N、C始终在PQ的两侧．设点P的运动时间为t（s）（t＞0）．
  （1）用含t的代数式表示DP的长；
  （2）当点N落在边AB上时，求t的值；
  （3）连结DQ，当∠PQD=∠A时，求PQ的长；
  （4）过点N作MN⊥AC于点M，取AD的中点O，作直线OQ，当直线OQ将线段MN分为1：3两部分时，直接写出t的值．
  组卷：205引用：2难度：0.2

  解析

• 24．在平面直角坐标系中，已知抛物线y=-x²+bx+c（b,c为常数）经过点（-1，0），（2，3）．
  （1）求抛物线的顶点坐标；
  （2）当点（a,y₁），

  （

  a

  +

  1

  2

  ，

  y

  2

  ）

  都在此抛物线上，且y₁＜y₂时，则a的取值范围是

  ；
  （3）当抛物线在直线x=-1-n与直线x=n之间（包括边界点）的图象的函数值y随x的增大而先增大再减小时，最高点的纵坐标与最低点的纵坐标的差为10，求n的值．
  （4）若点M在抛物线上，其横坐标为m,设点P的坐标为（-1，m-3），连结PM，当PM不与坐标轴平行时，以PM为对角线构造矩形PQMN，MQ∥x轴，当抛物线与矩形PQMN的边只有两个交点，且两交点与x轴的距离之和为

  9

  4

  时，直接写出m值．
  组卷：245引用：1难度：0.2

  解析