2022-2023学年辽宁省锦州市高二（下）期末数学试卷
发布：2024/6/27 8:0:9
一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
-
1．等差数列{an}中，a3=3，a7=27，则数列{an}的公差为（ ）
组卷：150引用：2难度：0.8 -
2．一箱产品中有6件正品和2件次品．每次从中随机抽取1件进行检测，抽出的产品不再放回．已知前两次检测的产品均是正品，则第三次检测的产品是正品的概率为（ ）
组卷：37引用：3难度：0.8 -
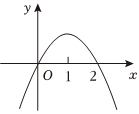3．已知函数y=f（x）的导函数f′（x）的图象如图所示，则f（x）的图象可能是（ ）组卷：277引用：3难度：0.8 -
4．某商场为了了解毛衣的月销售量y（件）与月平均气温x（℃）之间的关系，随机统计了某4个月的月销售量与当月平均气温，其数据如表：
由表中数据算出线性回归方程月平均气温x（℃） 17 13 8 2 月销售量y（件） 24 33 40 55 =bx+a中的b=-2，气象部门预测下个月的平均气温约为8℃，据此估计该商场下个月毛衣销售量约为（ ）件．̂y组卷：41引用：3难度：0.7 -
5．康托（Cantor）是十九世纪末二十世纪初德国伟大的数学家，他创立的集合论奠定了现代数学的基础．著名的“康托三分集”是数学理性思维的产物，具有典型的分形特征，其操作过程如下：将闭区间[0，1]均分为三段，去掉中间的区间段
，当记为第一次操作；再将剩下的两个区间（13，23）分别均分为三段，并各自去掉中间的区间段，记为第二次操作：…，如此这样，每次在上一次操作的基础上，将剩下的各个区间分别均分为三段，同样各自去掉中间的区间段．操作过程不断地进行下去，以至无穷，剩下的区间集合即是“康托三分集”．若使“康托三分集”的各区间长度之和小于[0，13]，[23，1]，则需要操作的次数n的最小值为（ ）（参考数据：lg2=0.3010，lg3=0.4771）120组卷：32引用：2难度：0.5 -
6．已知
，设曲线y=lnx3-x3在x=k,k＞0处的切线斜率为f（k），则（ ）a=2，b=log23，c=e2组卷：169引用：2难度：0.6 -
7．班级举行知识竞猜闯关活动，设置了A，B，C三个问题．答题者可自行决定答三题顺序．甲有60%的可能答对问题A，80%的可能答对问题B，50%的可能答对问题C．记答题者连续答对两题的概率为p,要使得p最大，他应该先回答（ ）
组卷：176引用：4难度：0.6
四、解答题：本题共6小题，共70分解答应写出文字说明、证明过程或演算步骤．
-
21．2022北京冬奥会和冬残奥会吉祥物冰墩墩、雪容融亮相上海展览中心、为了庆祝吉祥物在上海的亮相，某商场举办了一场赢取吉祥物挂件的“定点投篮”活动，方案如下：
方案一：共投9次，每次投中得1分，否则得0分，累计所得分数记为Y；
方案二：共进行三轮投篮，每轮最多投三次，直到投中两球为止得3分，否则得0分，三轮累计所得分数记为X．累计所得分数越多，所获得奖品越多．现在甲准备参加这个“定点投篮”活动，已知甲每次投篮的命中率为P，每次投篮互不影响．
（1）若p=，甲选择方案二，求第一轮投篮结束时，甲得3分的概率；12
（2）以最终累计得分的期望值为决策依据，甲在方案一，方案二之中选其一、应选择哪个方案？组卷：96引用：4难度：0.6 -
22．已知函数f（x）=
．a2x2-x-xlnx（a∈R）
（1）若a=2，求方程f（x）=0的解；
（2）若f（x）有两个零点且有两个极值点，记两个极值点为x1，x2，求a的取值范围并证明f（x1）+f（x2）＜．12e组卷：256引用：5难度：0.2
