2023年吉林省白山市抚松一中高考数学第十一次模拟试卷

一、单选题

• 1．已知z=2-i,则z（

  z

  +i）=（　　）

  A．6-2i

  B．4-2i

  C．6+2i

  D．4+2i
  组卷：5230引用：49难度：0.9

  解析

• 2．对方程

  y

  -

  6

  x

  +

  3

  =

  2

  表示的图形，下列叙述中正确的是（　　）

  A．斜率为2的一条直线

  B．斜率为 - 1 2 的一条直线

  C．斜率为2的一条直线，且除去点（-3，6）

  D．斜率为 - 1 2 的一条直线，且除去点（-3，6）
  组卷：418引用：3难度：0.7

  解析

• 3．与直线x+2y+1=0垂直，且与圆x²+y²=1相切的直线方程是（　　）

  A． 2 x + y + 5 = 0 或 2 x + y - 5 = 0	B．2x+y+5=0或2x+y-5=0
  C． 2 x - y + 5 = 0 或 2 x - y - 5 = 0	D．2x-y+5=0或2x-y-5=0
  组卷：260引用：1难度：0.5

  解析

• 4．已知f（x）=

  1

  1

  -

  x

  ，当x≠0时，在下列四式中与f[f（x）]的函数解析式相同的是（　　）

  A． 1 xf （ x ）

  B． 1 x + f （ x ）

  C．- 1 xf （ x ）

  D． 1 x - f （ x ）
  组卷：340引用：1难度：0.9

  解析

• 5．抚松县第一中学全体师生为庆祝2023年高考圆梦成功，选定大方鼎雕塑为吉祥物，为高考鼎立助威．若在B、C处分别测得雕塑最高点的仰角为30°和20°，且BC=5cm,则该雕塑的高度约为（　　）（参考数据cos10°=0.985）

  A．4.92

  B．5.076

  C．6.693

  D．7.177
  组卷：18引用：1难度：0.8

  解析

• 6．已知双曲线

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的一条渐近线的倾斜角为θ（其中θ为钝角），则双曲线C的离心率为（　　）

  A． 1 sinθ

  B． 1 cosθ

  C． - 1 sinθ

  D． - 1 cosθ
  组卷：151引用：4难度：0.8

  解析

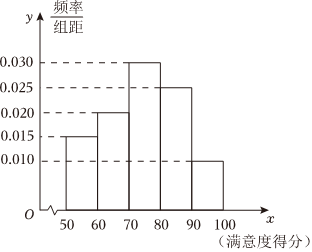• 7．近年来，网络消费新业态、新应用不断涌现，消费场景也随之加速拓展，某报社开展了网络交易消费者满意度调查，某县人口约为50万人，从该县随机选取5000人进行问卷调查，根据满意度得分分成以下5组：[50，60），[60，70），…，[90，100]，统计结果如图所示．由频率分布直方图可认为满意度得分X（单位：分）近似地服从正态分布N（μ，σ²），且P（μ-σ＜X＜μ+σ）≈0.6826，P（μ-2σ＜X＜μ+2σ）≈0.9544，P（μ-3σ＜X＜μ+3σ）≈0.9974，其中μ近似为样本平均数，σ近似为样本的标准差s,并已求得s=12．则（　　）

  A．由直方图可估计样本的平均数约为74.5

  B．由直方图可估计样本的中位数约为75

  C．由正态分布可估计全县X≥98.5的人数约为2.3万人

  D．由正态分布可估计全县62.5≤X＜98.5的人数约为40.9万人
  组卷：121引用：6难度：0.9

  解析

四、解答题

• 21．已知函数f（x）=asin2x+cos2x,且

  f

  （

  x

  ）

  ≤

  |

  f

  （

  -

  π

  6

  ）

  |

  ．
  （1）求f（x）的最大值；
  （2）从①②中任选一个作答．若选择多个分别作答．按第一个解答计分．
  ①A为函数f（x）图象与x轴的交点，点B，C为函数f（x）图象的最高点或者最低点，求△ABC面积的最小值．
  ②O为坐标原点，复数z₁=-2-4i,z₂=-2+f（t）i在复平面内对应的点分别为A，B，求△OAB面积的取值范围．
  组卷：49引用：3难度：0.6

  解析

• 22．帕德近似是法国数学家亨利•帕德发明的用有理多项式近似特定函数的方法．给定两个正整数m,n,函数f（x）在x=0处的[m,n]阶帕德近似定义为：

  R

  （

  x

  ）

  =

  a

  0

  +

  a

  1

  x

  +

  ⋯

  +

  a

  m

  x

  m

  1

  +

  b

  1

  x

  +

  ⋯

  +

  b

  n

  x

  n

  ，且满足：f（0）=R（0），f'（0）=R'（0），f″（0）=R″（0）…，f^（m+n）（0）=R^（m+n）（0）．已知f（x）=ln（x+1）在x=0处的[1，1]阶帕德近似为

  R

  （

  x

  ）

  =

  ax

  1

  +

  bx

  ．
  注：f″（x）=[f'（x）]′，f″'（x）=[f″（x）]′，f^（4）（x）=[f″'（x）]′，f^（5）（x）=[f^（4）（x）]′，…
  （1）求实数a,b的值；
  （2）求证：

  （

  x

  +

  b

  ）

  f

  （

  1

  x

  ）

  ＞

  1

  ；
  （3）求不等式

  （

  1

  +

  1

  x

  ）

  x

  ＜

  e

  ＜

  （

  1

  +

  1

  x

  ）

  x

  +

  1

  2

  的解集，其中e=2.71828⋯．
  组卷：222引用：12难度：0.2

  解析