当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省泰州市姜堰区七年级（下）期末数学试卷

发布：2024/7/3 8:0:9

一、选择题（本大题共6小题，每小题3分，共18分。在每小题所给出的四个选项中，只有一项是正确的，请把正确选项前的字母代号填涂在答题卡相应位置上）

1．下列图形是我国几所大学的校徽，其中运用了“平移”制作的是（　　）#ZZ04
A．
北京大学 B．
复旦大学
C．
中国人民大学 D．
南开大学
组卷：48引用：1难度：0.7
解析
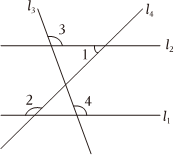2．如图，∠1与∠2互为补角，∠3=117°，则∠4的度数是（　　）

A．117° B．63° C．100° D．80°
组卷：96引用：1难度：0.7
解析
3．若a＞b,则下列式子正确的是（　　）
A．-2023a＞-2023b B．2023a＜2023b
C．2023-a＞2023-b D．a-2023＞b-2023
组卷：149引用：3难度：0.7
解析
4．下列命题中，假命题的是（　　）
A．对顶角相等
B．同位角相等
C．直角三角形的两个锐角互余
D．三角形的外角和等于360°
组卷：108引用：3难度：0.9
解析
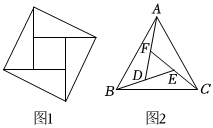5．大约在公元222年，赵爽为《周髀算经》一书作序时，介绍了“勾股圆方图”，亦称“赵爽弦图”（如图1），某数学兴趣小组类比“赵爽弦图”构造出图2：△ABC为等边三角形，AD、BE、CF围成的△DEF也是等边三角形．已知点D、E、F分别是BE、CF、AD的中点，若△ABC的面积为14，则△DEF的面积是（　　）
A．1 B．2 C．3 D．4
组卷：711引用：12难度：0.5
解析
6．已知关于x、y的二元一次方程（m+1）x+（2-m）y-4m+2=0，当m每取一个值时，就有一个对应的方程，而这些方程有一个公共解，则这个公共解是（　　）
A．
x
=
0
y
=
2
B．
x
=
1
y
=
2
C．
x
=
-
1
y
=
0
D．
x
=
2
y
=
-
2
组卷：515引用：2难度：0.7
解析

二、填空题（本大题共10小题，每小题3分，共30分。不需要写出解答过程，只需把答案直接填写在答题卡相应位置上）

7．a⁵÷a³=
．
组卷：763引用：6难度：0.9
解析
8．五边形的外角和为
．
组卷：347引用：24难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共10小题，共102分。请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）

25．某数学实验小组在探究“关于x的二次三项式ax²+bx+3的性质（a、b为常数）”时，进行了如下活动．
（1）【实验操作】
取不同的x的值，计算代数式ax²+bx+3的值．

x … -2 -1 0 1 …

ax²+bx+3 … 11 6 3 2 …

根据表格，计算出a、b的值；
（2）【观察猜想】
实验小组组员通过观察表格，提出以下猜想：
①代数式ax²+bx+3的值随着x的增大而减小；
②当x=1时，代数式ax²+bx+3有最小值，最小值是2．
上述猜想中正确的是：
；（填写序号）
（3）【验证猜想】
请对正确的猜想进行证明；
（4）【归纳运用】
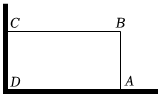
根据实验经验解决下列问题：
如图所示，小丽想借助院中互相垂直的两面墙（墙体足够长），在墙角区域用6m长的篱笆围成一个长方形小菜园．当AB为何值时，长方形小菜园ABCD的面积最大，并求出最大面积．
组卷：387引用：2难度：0.5
解析
26．已知l₁∥l₂，李想同学将△ABC放置在这两条平行线上展开探究，其中△ABC三边与两条平行线分别交于点D、E、F、G．
（1）【特例探究】如图1，∠C=90°．
①∠CED+∠CGF=
度；
②若∠CED与∠CGF的角平分线相交于点P，则∠EPG=
度；
（2）【一般探索】如图2，∠C=α，∠EPG=β．
①若∠DEP=
1
3
∠CED，∠FGP=
1
3
∠CGF，求α与β的关系；
②若∠DEP=
1
n
∠CED，∠FGP=
1
n
∠CGF（n≥2且n为整数），直接写出α与β的关系
；
（3）【拓展应用】如图3，∠CED与∠CGF的角平分线相交于点P₁，∠P₁ED与∠P₁GF的角平分线相交于点P₂，∠P₂ED与∠P₂GF的角平分线相交于点P₃；…，以此类推，则
360
°
-
∠
C
∠
E
P
2023
G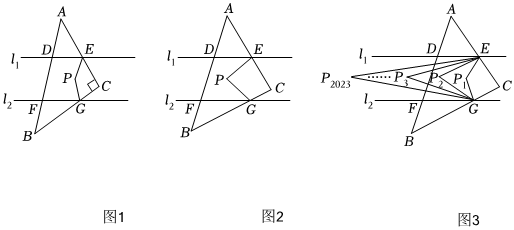
的值是多少？（直接写出结果）

组卷：514引用：3难度：0.4
解析