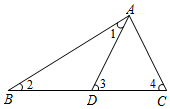
已知l₁∥l₂，李想同学将△ABC放置在这两条平行线上展开探究，其中△ABC三边与两条平行线分别交于点D、E、F、G．
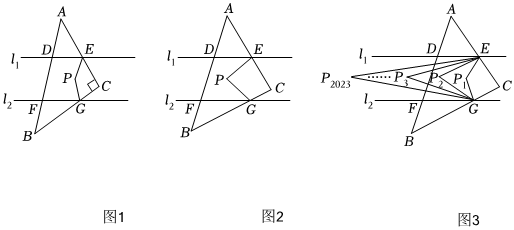
（1）【特例探究】如图1，∠C=90°．
①∠CED+∠CGF=

270

270

度；
②若∠CED与∠CGF的角平分线相交于点P，则∠EPG=

135

135

度；
（2）【一般探索】如图2，∠C=α，∠EPG=β．
①若∠DEP=

1

3

∠CED，∠FGP=

1

3

∠CGF，求α与β的关系；
②若∠DEP=

1

n

∠CED，∠FGP=

1

n

∠CGF（n≥2且n为整数），直接写出α与β的关系

α+nβ=360°

α+nβ=360°

；
（3）【拓展应用】如图3，∠CED与∠CGF的角平分线相交于点P₁，∠P₁ED与∠P₁GF的角平分线相交于点P₂，∠P₂ED与∠P₂GF的角平分线相交于点P₃；…，以此类推，则

360

°

-

∠

C

∠

E

P

2023

G

的值是多少？（直接写出结果）
​