2022-2023学年福建省厦门市思明区松柏中学八年级（下）期末数学试卷

一、选择题（每小题4分，共40分，每小题都有四个选项，其中有且只有一个选项正确）

• 1．下列二次根式是最简二次根式的是（　　）

  A． 3

  B． 0 . 25

  C． 1 2

  D． 8
  组卷：50引用：1难度：0.7

  解析

• 2．方程（x-1）（x+2）=0的解是（　　）

  A．x1=1，x2=2	B．x1=-1，x2=2
  C．x1=1，x2=-2	D．x1=-1，x2=-2
  组卷：1062引用：18难度：0.9

  解析

• 3．下列四组数据中，不能作为直角三角形的三边长的是（　　）

  A．5，12，13

  B．6，8，10

  C． 1 ， 1 ， 2

  D．3，4，6
  组卷：48引用：1难度：0.7

  解析

• 4．若▱ABCD对角线AC，BD相交于点O，点E是BC中点，若OE=3，则AB长为（　　）

  A．3

  B．6

  C．9

  D．12
  组卷：56引用：4难度：0.7

  解析

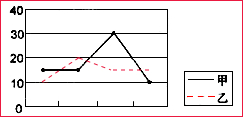• 5．如图是甲、乙两组数据的折线统计图，下列结论中正确的是（　　）

  A．甲组数据比乙组数据稳定

  B．乙组数据比甲组数据稳定

  C．甲、乙两组数据一样稳定

  D．不能比较两组数据的稳定性
  组卷：137引用：15难度：0.9

  解析

• 6．矩形ABCD中，对角线AC，BD交于点O．若∠COB=120°，BD=8，则AB的长为（　　）

  A．4

  B． 4 3

  C．3

  D．5
  组卷：70引用：1难度：0.7

  解析

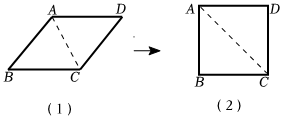• 7．小明用四根长度相等的木条制作了能够活动的菱形学具，他先活动学具成为图（1）所示的菱形，并测得∠B=60°，接着活动学具成为图（2）所示的正方形，并测得对角线AC=20

  2

  ，则图（1）中菱形的对角线BD长为（　　）

  A．20

  B．30

  C． 20 3

  D． 20 2
  组卷：918引用：10难度：0.5

  解析

• 8．已知一次函数y=kx+b,函数值y随自变量x的减小而增大，且k+b＞0，则函数y=kx+b的图象大致是（　　）

  A．

  B．

  C．

  D．
  组卷：186引用：1难度：0.5

  解析

三、解答题（本大题共9个小题，共86分）

• 24．如图1，在正方形ABCD中，F是BC的中点，连接AF，过点D作DE⊥AF于点G，交AB于点E，过点B作BM⊥AF于点M．
  （1）求证：E为AB的中点；
  （2）求证：AG=GM；
  （3）如图2，连接DM，作∠CDM的平分线交BC于点N，求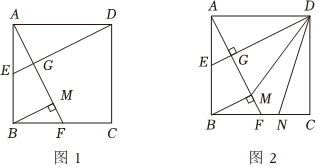

  CN

  DM

  的值．
  
  组卷：104引用：1难度：0.2

  解析

• 25．在平面直角坐标系中，对于任意两点A（x₁，y₁）和B（x₂，y₂），称点（x₁x₂，y₁y₂）为点A和B的融合点．如（2，3）和（1，4）的融合点是（2，12）．
  （1）点（3，2）和（0.5，6）的融合点坐标是

  ；
  （2）已知点P（3，1）和直线l：y=-2x+4．设点Q是直线l上任意一点，点P和Q的融合点为点T．
  ①求证：当点Q在直线l上移动时，点T始终在同一条直线上．
  ②若

  M

  （

  -

  1

  ，

  0

  ）

  ，

  N

  （

  0

  ，-

  2

  3

  ）

  ，求△MNT的面积．
  （2）对于点C（m,n）（mn≠0）和直线h：y=kx+b（k≠0），点D是直线h上任意一点，类似（2），可证明当点D在直线h上移动时，点C和D的融合点始终在同一条直线上，称该直线为点C和直线h的融合直线．已知直线s：y=3x+4，点R在直线x=2上且纵坐标不为0，点R和直线s的融合直线记为t.点E（-2，2）点F（2，-2），若融合直线t与线段EF有公共点，请直接写出点R的纵坐标y_R的取值范围．
  组卷：254引用：1难度：0.3

  解析