2022-2023学年浙江省杭州市高一（下）期末数学试卷

一、选择题（本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中只有一项是符合题目要求的.）

• 1．已知集合A={1，2，3，4}，B={x|x²-2x-3≤0}，则A∩B=（　　）

  A．{1}

  B．{1，2}

  C．{1，2，3}

  D．{1，2，3，4}
  组卷：55引用：5难度：0.9

  解析

• 2．若z•i=2+3i（i是虚数单位），则|z|=（　　）

  A．2

  B．3

  C． 13

  D． 3 2
  组卷：87引用：4难度：0.8

  解析

• 3．军事上角的度量常用密位制，密位制的单位是“密位”1密位就是圆周的

  1

  6000

  所对的圆心角的大小，．若角α=1000密位，则α=（　　）

  A． π 6

  B． π 4

  C． π 3

  D． 5 π 12
  组卷：142引用：4难度：0.7

  解析

• 4．已知平面α⊥平面β，直线l⊄α，则“l⊥β”是“l∥α”的（　　）

  A．充分而不必要条件	B．必要而不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：266引用：9难度：0.5

  解析

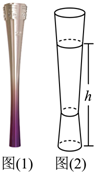• 5．杭州亚运会火炬如图（1）所示，小红在数学建模活动时将其抽象为图（2）所示的几何体．假设火炬装满燃料，燃烧时燃料以均匀的速度消耗，记剩余燃料的高度为h,则h关于时间t的函数的大致图象可能是（　　）

  A．

  B．

  C．

  D．
  组卷：100引用：4难度：0.8

  解析

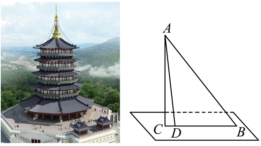• 6．雷峰塔位于杭州市西湖景区，主体为平面八角形体仿唐宋楼阁式塔，总占地面积3133平方米，项目学习小组为了测量雷峰塔的高度，如图选取了与底部水平的直线BC，测得∠ABC、∠ADC的度数分别为α、β，以及D、B两点间的距离d,则塔高AC=（　　）

  A． dsinαsinβ sin （ β - α ）	B． dsinαsinβ cos （ β - α ）
  C． dtanαtanβ tan （ β - α ）	D． dsinαcosβ sin （ β - α ）
  组卷：136引用：2难度：0.7

  解析

• 7．已知函数

  f

  （

  x

  ）

  =

  ex

  +

  π

  ，

  g

  （

  x

  ）

  =

  （

  π

  e

  ）

  x

  （e为自然对数的底数），则（　　）

  A．∀x∈（0，+∞），f（x）＞g（x）

  B． ∃ x 0 ∈ （ e π ， eπ ） ，当x=x0时，f（x）=g（x）

  C． ∀ x ∈ （ e π ， eπ ） ， f （ x ） ＜ g （ x ）

  D． ∃ x 0 ∈ （ e 2 π ， + ∞ ） ，当x＞x0时，f（x）＜g（x）
  组卷：105引用：1难度：0.5

  解析

三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）

• 21．生活中为了美观起见，售货员用彩绳对长方体礼品盆进行捆扎．有以下两种捆扎方案：方案（1）为十字捆扎（如图（1）），方案（2）为对角捆扎（如图（2））．设礼品盒的长AB，宽BC，高AA₁分别为30cm,20cm,10cm.
  
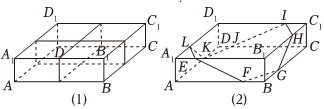
  （1）在方案（2）中，若LA₁=A₁E=IC₁=C₁H=FB=BG=10cm,设平面LEF与平面GHI的交线为l,求证：l∥平面ABCD；
  （2）不考虑花结用绳，对于以上两种捆扎方式，你认为哪一种方式所用彩绳最少，最短绳长为多少cm？
  组卷：106引用：3难度：0.5

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  x

  +

  1

  x

  （

  x

  ＞

  0

  ）

  ，

  g

  （

  x

  ）

  =

  x

  （

  x

  ＞

  0

  ）

  ．
  （1）直接写出|f（x）-g（x）|＜|g（x）-f（x）+1|的解集；
  （2）若f（x₁）=f（x₂）=g（x₃），其中x₁＜x₂，求f（x₁+x₂）+g（x₃）的取值范围；
  （3）已知x为正整数，求h（x）=（m+1）x²-2（m²+1）x（m∈N^*）的最小值（用m表示）．
  组卷：203引用：2难度：0.4

  解析