当前位置：试卷中心 > 试卷详情

2022-2023学年广东省佛山市南海外国语学校九年级（上）期中数学试卷

发布：2024/9/25 0:0:1

一、选择题（共10小题，每小题3分，共30分）

1．如图，该几何体的左视图为（　　）
A． B． C． D．
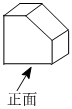组卷：19引用：1难度：0.8
解析
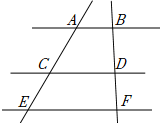2．如图，AB∥CD∥EF，AC：CE=3：2，BD=6，则DF的长为（　　）
A．2 B．4 C．9 D．10
组卷：391引用：5难度：0.5
解析
3．一元二次方程2x²-7x-1=0的根的情况是（　　）
A．有两个不相等的实数根 B．有两个相等的实数根
C．没有实数根 D．不能确定
组卷：777引用：12难度：0.8
解析
4．若方程（m-2）
x
m
2
-
2
+3x-2=0是关于x的一元二次方程，则m的值是（　　）
A．2 B．-2 C．±2 D．0
组卷：223引用：7难度：0.8
解析
5．在不透明的袋子中装有黑、白两种球共50个，这些球除颜色外都相同，随机从袋中摸出一个球，记录下颜色后，放回袋子中并摇匀，再从中摸出一个球，经过如此大量重复试验，发现摸出的黑球的频率稳定在0.4附近，则袋子中黑球的个数约为（　　）
A．20个 B．30个 C．40个 D．50个
组卷：376引用：8难度：0.6
解析
6．某乐器上的一根弦AB=80cm,两个端点A、B固定在乐器面板上，支撑点C是AB的黄金分割点，且AC＞BC，则AC的长（　　）
A．40（
5
-
1
）cm B．40（
5
+1）cm C．40（3-
5
）cm D．40（3+
5
）cm
组卷：250引用：2难度：0.6
解析
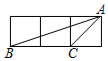7．如图，每个小正方形边长均为1，则图中四个阴影的三角形中与△ABC相似的是（　　）
A． B． C． D．
组卷：109引用：2难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共8小题，16、17、18题每题8分，19、20、21题每题9分，22、23题每题12分，共75分）

22．阅读材料：把形如x²+bx+c的二次三项式（或其一部分）配成完全平方式的方法叫做配方法，配方法的基本形式是完全平方公式的逆写，即a²±2ab+b²=（a±b）²．
例如：x²-2x+4=x²-2x+1+3=（x-1）²+3；
x²-2x+4=x²-4x+4+2x=（x-2）²+2x；
x²-2x+4=
1
4
x
2
-
2
x
+
4
+
3
4
x
2
=
（
1
2
x
-
2
）
2
+
3
4
x
2
；
是x²-2x+4的三种不同形式的配方（即“余项”分别是常数项、一次项、二次项）．
请根据阅读材料解决下列问题：
（1）比照上面的例子，将二次三项式x²-6x+16配成完全平方式（直接写出两种形式）；
（2）已知a、b、c是△ABC的三边，且满足a²+2b²+c²-2b（a+c）=0，试判断此三角形的形状并说明理由；
（3）已知2x+y=6，求当x、y分别取什么值时，x²+2xy+y²-3x-2y取最小值，最小值是多少？
组卷：81引用：2难度：0.5
解析
23．【感知】
如图1，在四边形ABCD中，点P在边AB上（不与A、B重合），∠A=∠B=∠DPC=90°．易证：△DAP∽△PBC（不要求证明）．
【探究】
如图2，在四边形ABCD中，点P在边AB上（点P不与点A、B重合），∠A=∠B=∠DPC．
（1）求证：△DAP∽△PBC．
（2）若PD=5，PC=10，BC=9，则AP的长为
．
【应用】
如图3，在△ABC中，AC=BC=8，AB=12．点P在边AB上（点P不与点A、B重合），连结CP，作∠CPE=∠A，PE与边BC交于点E．
（3）当CE=3EB时，求AP的长．
（4）当△CPE是等腰三角形时，直接写出AP的长．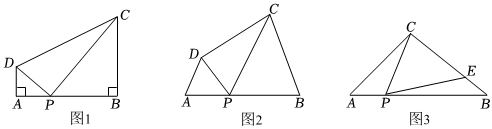
组卷：122引用：2难度：0.5
解析