2023-2024学年河南省开封市祥符高级中学高二（上）第一次月考数学试卷

一、单选题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．在空间直角坐标系中，已知两点坐标A（1，-1，1），B（0，2，-1），则AB=（　　）

  A． 14

  B． 3

  C．3

  D．1
  组卷：170引用：3难度：0.8

  解析

• 2．已知直线l的倾斜角为150°，则l的斜率为（　　）

  A． 3

  B． 3 3

  C．- 3

  D．- 3 3
  组卷：48引用：6难度：0.9

  解析

• 3．若直线l的方向向量为

  a

  =

  （

  3

  ，-

  1

  ，

  2

  ）

  ，平面α的法向量为

  n

  =

  （

  -

  6

  ，

  2

  ，-

  4

  ）

  ，则（　　）

  A．l⊥α

  B．l∥α

  C．l⊂α

  D．l与α斜交
  组卷：59引用：2难度：0.8

  解析

• 4．正四面体O-ABC棱长为1，E为BC中点，则

  OE

  •

  AB

  =（　　）

  A． - 1 2

  B． 1 4

  C． - 1 4

  D． 1 2
  组卷：227引用：4难度：0.7

  解析

• 5．以A（-1，1），B（2，-1），C（1，4）为顶点的三角形是（　　）

  A．钝角三角形

  B．锐角三角形

  C．以A为直角的直角三角形

  D．以C为直角的直角三角形
  组卷：9引用：2难度：0.7

  解析

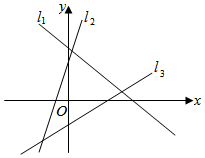• 6．如图，设直线l₁，l₂，l₃的斜率分别为k₁，k₂，k₃，则k₁，k₂，k₃的大小关系为（　　）

  A．k1＜k2＜k3

  B．k2＜k1＜k3

  C．k3＜k2＜k1

  D．k1＜k3＜k2
  组卷：109引用：5难度：0.7

  解析

• 7．在正方体ABCD-A₁B₁C₁D₁中，P，Q分别为BC，A₁B₁的中点，则异面直线PQ与A₁C₁所成角的正弦值为（　　）

  A． 2 2 3

  B． 1 3

  C． 6 3

  D． 3 3
  组卷：31引用：3难度：0.5

  解析

四、解答题：每小题10分，共6小题，共50分.

• 21．已知过点P（m,n）的直线l与直线l₀：x+2y+4=0垂直．
  （Ⅰ）若

  m

  =

  1

  2

  ，且点P在函数

  y

  =

  1

  1

  -

  x

  的图象上，求直线l的一般式方程；
  （Ⅱ）若点P（m,n）在直线l₀上，判断直线mx+（n-1）y+n+5=0是否经过定点？若是，求出该定点的坐标；否则，请说明理由．
  组卷：349引用：4难度：0.5

  解析

• 22．已知三棱锥P-ABC（如图①）的平面展开图（如图②）中，四边形ABCD为边长为

  2

  2

  的正方形，△ABE和△BCF均为正三角形．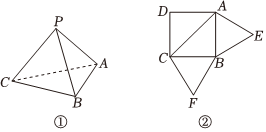
  
  （1）证明：平面PAC⊥平面ABC；
  （2）棱PA上是否存在一点M，使平面PBC与平面BCM所成角的余弦值为

  2

  2

  3

  ，若存在，求出

  PM

  PA

  的值；若不存在，请说明理由．
  组卷：61引用：5难度：0.4

  解析