2022-2023学年四川省成都市树德中学光华校区高一（下）期末数学模拟试卷（1）

一、单选题（共40分）

• 1．已知向量

  a

  =（1，0），

  b

  =（1，1），若

  a

  +λ

  b

  与λ

  a

  +

  b

  共线，则实数λ的值为（　　）

  A．-1

  B．1

  C．±1

  D．0
  组卷：277引用：5难度：0.7

  解析

• 2．将正弦函数f（x）=sinx的图象先向左平移

  π

  3

  个单位长度，再将得到的图象上所有点的横坐标缩短到原来的

  1

  2

  ，纵坐标不变，最后得到函数g（x）的图象，则g（x）=（　　）

  A． g （ x ） = sin （ 2 x + 2 π 3 ）	B． g （ x ） = sin （ 2 x + π 3 ）
  C． g （ x ） = sin （ x 2 + π 3 ）	D． g （ x ） = sin （ x 2 + π 6 ）
  组卷：847引用：7难度：0.9

  解析

• 3．在△ABC中，角A，B，C所对的边分别为a,b,c.已知a=

  2

  ，b=

  3

  ，

  B

  =

  π

  3

  ，则角A为（　　）

  A． 3 π 4

  B． π 3

  C． π 4

  D． π 4 或 3 π 4
  组卷：360引用：6难度：0.7

  解析

• 4．已知α，β是两个不重合的平面，m,n是两条不同的直线，则下列命题正确的是（　　）

  A．若m⊥α，n⊥β，m⊥n,则α⊥β	B．若m∥α，n∥β，m∥n,则α∥β
  C．若m∥α，n⊂β，α∥β，则m∥n	D．若m∥α，n∥β，α⊥β，则m⊥n
  组卷：189引用：5难度：0.6

  解析

• 5．在四面体ABCD中，AB=CD，且异面直线AB与CD所成的角为70°，M，N分别是边BC，AD的中点，则异面直线MN和AB所成的角为（　　）

  A．35°

  B．55°

  C．35°或55°

  D．20°或70°
  组卷：102引用：2难度：0.7

  解析

• 6．已知等边三角形SAB为圆锥的轴截面，AB为圆锥的底面直径，O，C分别是AB，SB的中点，过OC且与平面SAB垂直的平面记为α，若点S到平面α的距离为

  6

  ，则该圆锥的侧面积为（　　）

  A．8π

  B．16π

  C．24π

  D．32π
  组卷：121引用：3难度：0.6

  解析

• 7．已知正方体ABCD-A₁B₁C₁D₁的棱长为1，E为DD₁中点，F为棱CD上异于端点的动点，若平面BEF截该正方体所得的截面为四边形，则线段CF的取值范围是（　　）

  A．（ 1 3 ，1）

  B．（ 1 2 ，1）

  C．[ 1 2 ， 2 3 ）

  D．（0， 1 2 ]
  组卷：92引用：4难度：0.6

  解析

四、解答题（共70分）

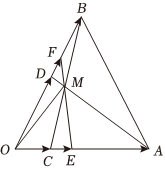• 21．如图所示，在△ABO中，

  OC

  =

  1

  4

  OA

  ，

  OD

  =

  1

  2

  OB

  ，AD与BC相交于点M，设

  OA

  =

  a

  ，

  OB

  =

  b

  ．
  （1）试用向量

  a

  ，

  b

  表示

  OM

  ；
  （2）过点M作直线EF分别交线段AC，BD于点E，F，记

  OE

  =

  λ

  OA

  ，

  OF

  =

  μ

  OB

  ，求证：不论点E，F在线段AC，BD上如何移动，

  1

  λ

  +

  3

  μ

  为定值．
  组卷：433引用：8难度：0.7

  解析

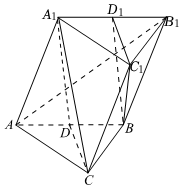• 22．如图，在斜三棱柱ABC-A₁B₁C₁中，AC=BC，D为AB的中点，D₁为A₁B₁的中点，平面A₁B₁C₁⊥平面ABB₁A₁，异面直线BC₁与AB₁互相垂直．
  （1）求证：平面A₁DC∥平面BD₁C₁；
  （2）若CC₁与平面ABB₁A₁的距离为x,A₁C=AB₁=6，三棱锥A₁-ACD的体积为y,试写出y关于x的函数关系式；
  （3）在（2）的条件下，当CC₁与平面ABB₁A₁的距离为多少时，三棱锥A₁-ACD的体积取得最大值？并求出最大值．
  组卷：471引用：4难度：0.3

  解析