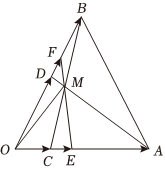
如图所示，在△ABO中，OC=14OA，OD=12OB，AD与BC相交于点M，设OA=a，OB=b．
（1）试用向量a，b表示OM；
（2）过点M作直线EF分别交线段AC，BD于点E，F，记OE=λOA，OF=μOB，求证：不论点E，F在线段AC，BD上如何移动，1λ+3μ为定值．
OC
=
1
4
OA
OD
=
1
2
OB
OA
=
a
OB
=
b
a
，
b
OM
OE
=
λ
OA
OF
=
μ
OB
1
λ
+
3
μ
【考点】用平面向量的基底表示平面向量．
【答案】（1）=+，
（2）证明详见解析．
OM
1
7
a
3
7
b
（2）证明详见解析．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/9 8:0:9组卷：441引用：8难度：0.7
相似题
-
1．如图，在△OAB中，G为中线OM上一点，且，过点G的直线与边OA，OB分别交于点P，Q．OG=2GM
（Ⅰ）用向量，OA表示OB；OG
（Ⅱ）设向量，OA=43OP，求n的值．OB=nOQ发布：2024/12/29 8:30:1组卷：682引用：6难度：0.7 -
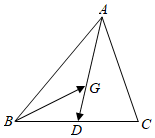2．如图，在△ABC中，点D是边BC的中点，，则用向量AG=2GD表示AB，AC为（ ）BG发布：2024/12/29 8:30:1组卷：732引用：13难度：0.8 -
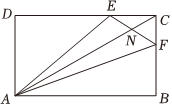3．如图矩形ABCD，，DE=2EC，AC与EF交于点N．BF=2FC
（1）若，求λ+μ的值；CN=λAB+μAD
（2）设，AE=a，试用AF=b，a表示b．AC发布：2024/12/29 4:30:2组卷：20引用：2难度：0.6
