当前位置：试卷中心 > 试卷详情

2023-2024学年北京市怀柔一中高二（上）开学数学试卷

发布：2024/8/3 8:0:9

一、选择题

1．已知
a
=（1，2），
b
=（4，-2），下列说法正确的是（　　）
A．
|
a
|
=
3
B．
a
⊥
b
C．
a
∥
b
D．
b
-
a
=
（
3
，
4
）
组卷：146引用：4难度：0.8
解析
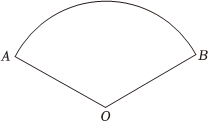2．扇子具有悠久的历史，蕴含着丰富的数学元素．小明制作了一把如图所示的扇子，其半径为16cm,圆心角为135°，则这把扇子的弧长为（　　）
A．6πcm B．12πcm C．18πcm D．24πcm
组卷：219引用：1难度：0.7
解析
3．已知
cosα
=
-
5
5
，α∈
（
π
2
，
π
）
，则
tan
（
π
4
+
α
）
=（　　）
A．
1
3
B．3 C．-3 D．
-
1
3
组卷：282引用：3难度：0.8
解析
4．下列函数中，最小正周期为π且是偶函数的是（　　）
A．
y
=
sin
（
x
+
π
2
）
B．y=tanx
C．y=cos2x D．y=sin2x
组卷：42引用：1难度：0.7
解析
5．在平行四边形ABCD中，M是DC的中点，向量
DN
=
2
NB
，设
AB
=
a
，
AD
=
b
，则
MN
=（　　）
A．
1
6
a
-
2
3
b
B．-
1
6
a
+
1
3
b
C．
1
6
a
+
7
6
b
D．
1
6
a
-
1
3
b
组卷：634引用：4难度：0.8
解析
6．将函数y=sin（2x）的图象沿x轴向右平移φ（φ＞0）个单位长度，得到函数
y
=
sin
（
2
x
-
π
3
）
的图象，则φ的最小值为（　　）
A．
φ
=
π
6
B．
φ
=
π
3
C．
φ
=
2
π
3
D．
φ
=
5
π
6
组卷：159引用：2难度：0.6
解析
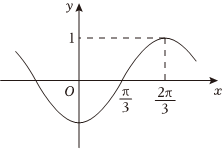7．已知函数f（x）=sin（ωx+φ）（ω＞0、|φ|＜π）的部分图象如图所示，则
f
（
π
6
）
=（　　）
A．
3
2
B．-
2
2
C．0 D．
2
2
组卷：650引用：5难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题

20．在△ABC中，角A，B，C的对边分别为a,b,c,已知
cos
A
=
-
1
4
，
b
=
4
．
（1）当
a
=
2
6
时，求△ABC的面积；
（2）再从下列三个条件中选择一个作为已知，使得三角形存在且唯一确定，并求a的值．
条件①：acosA=bcosB；
条件②：
2
sin
2
C
=
6
cos
C
；
条件③：
3
a
=
bsin
C
+
3
bcos
C
．
组卷：105引用：4难度：0.5
解析
21．如图，在四棱锥S-ABCD中，平面SAD⊥平面ABCD，SA=SD=AD=2，四边形ABCD为正方形，E为AD的中点，F为SB上一点，M为BC上一点，且平面EFM∥平面SCD．
（1）求证：M为线段BC中点；
（2）求证：平面SAD⊥平面SCD；
（3）在棱SC上是否存在点N，使得平面DMN⊥平面ABCD？若存在，求
CN
CS
；若不存在，说明理由．
组卷：128引用：2难度：0.5
解析