2022-2023学年重庆一中高一(下)期末数学试卷
发布:2024/5/29 8:0:9
一、单项选择题(本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合要求的)
-
1.已知i为虚数单位,复数z=(a2-1)+(a+1)i(a∈R)为纯虚数,则|z|=( )
组卷:38引用:1难度:0.7 -
2.直线
的倾斜角为( )x-3y+1=0组卷:629引用:20难度:0.9 -
3.平面向量
,a满足b,|a|=2,向量|b|=1与a的夹角为b,则23π=( )|a+2b|组卷:78引用:1难度:0.7 -
4.已知直线ax+2y+6=0与直线x+(a-1)y+a2-1=0互相平行,则实数a的值为( )
组卷:567引用:8难度:0.8 -
5.已知正三棱柱ABC-A1B1C1中,AB=2,AA1=1,点D为AB中点,则异面直线BC与C1D所成角的余弦值为( )
组卷:155引用:4难度:0.6 -
6.设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
组卷:66引用:3难度:0.7 -
7.在棱长为2的正方体ABCD-A1B1C1D1中,M为AB的中点,过点M的平面α截正方体ABCD-A1B1C1D1的外接球的截面面积的最小值为( )
组卷:123引用:1难度:0.5
四、解答题(共70分.解答应写出必要的文字说明,证明过程或演算步骤)
-
21.已知锐角△ABC的角A、B、C对边分别是a、b、c,且满足
.3sinA+cosA=b+ac
(1)求角C的大小;
(2)若,求c=3的取值范围.AB•BC+BC•CA+CA•AB组卷:54引用:1难度:0.5 -
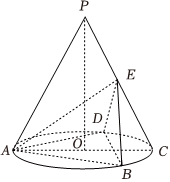 22.如图,P为圆锥的顶点,O是圆锥底面的圆心,AC为底面直径,△ABD为底面圆O的内接正三角形,且△ABD的边长为,点E在母线PC上,且3,CE=1.AE=3
22.如图,P为圆锥的顶点,O是圆锥底面的圆心,AC为底面直径,△ABD为底面圆O的内接正三角形,且△ABD的边长为,点E在母线PC上,且3,CE=1.AE=3
(1)求证:直线PO∥平面BDE,并求三棱锥P-BDE的体积:
(2)若点M为线段PO上的动点,当直线DM与平面ABE所成角的正弦值最大时,求此时点M到平面ABE的距离.组卷:115引用:5难度:0.5


