2023-2024学年上海市徐汇区南模中学高二（上）反馈练习数学试卷（9月份）

一、填空题（第1-6题每题4分，第7-12题每题5分，满分48分）

• 1．复数z满足z（1+i）=2i,则Imz=

  ．
  组卷：25引用：5难度：0.8

  解析

• 2．已知cosα=-

  3

  3

  ，且π＜α＜

  3

  π

  2

  ，则tanα=

   

  ．
  组卷：202引用：5难度：0.9

  解析

• 3．已知

  向量

  a

  =

  （

  m

  +

  1

  ，-

  3

  ）

  ，

  向量

  b

  =

  （

  1

  ，

  m

  -

  1

  ）

  ，

  若

  （

  a

  +

  b

  ）

  ⊥

  （

  a

  -

  b

  ）

  ，则实数m=

  ．
  组卷：112引用：7难度：0.7

  解析

• 4．已知数列{a_n}的前n项和S_n=-2n²+3n+1，则a_n=

  ．
  组卷：219引用：5难度：0.7

  解析

• 5．设方程x²-2x+m=0的两个根为α、β，且|α-β|=2，则实数m的值是

  ．
  组卷：89引用：7难度：0.7

  解析

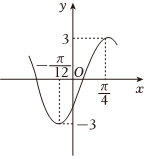• 6．已知函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜

  π

  2

  ）的部分图像如图所示，则此函数的表达式为

  ．
  组卷：203引用：7难度：0.7

  解析

• 7．已知A（-1，1）、B（1，2）、C（-2，-1）、D（3，4），则向量

  AB

  在

  CD

  方向上的投影向量为

  ．
  组卷：14引用：1难度：0.8

  解析

三、解答题（本大题共有5题，满分0分）

• 20．已知

  f

  （

  x

  ）

  =

  4

  sinxcos

  （

  x

  +

  π

  3

  ）

  +

  3

  ．
  （1）将f（x）化成

  A

  sin

  （

  ωx

  +

  φ

  ）

  +

  B

  （

  A

  ＞

  0

  ，

  ω

  ＞

  0

  ，

  |

  φ

  |

  ＜

  π

  2

  ）

  ；
  （2）求函数y=f（x）在区间

  [

  -

  π

  4

  ，

  π

  6

  ]

  上的单调减区间；
  （3）将函数y=f（x）的图像向右移动

  π

  6

  个单位，再将所得图像的上各点的横坐标缩短到原来的a（0＜a＜1）倍得到y=g（x）的图像，若y=g（x）在区间[-1，1]上至少有100个最大值，求实数a的取值范围．
  组卷：199引用：3难度：0.5

  解析

• 21．已知数列{a_n}：1，-2，-2，3，3，3，-4，-4，-4，-4，…，

  k

  个

  （

  -

  1

  ）

  k

  -

  1

  k

  ,…，

  （

  -

  1

  ）

  k

  -

  1

  k

  ，即当

  （

  k

  -

  1

  ）

  k

  2

  ＜

  n

  ≤

  k

  （

  k

  +

  1

  ）

  2

  （k∈N^*）时，

  a

  n

  =

  （

  -

  1

  ）

  k

  -

  1

  k

  ，记S_n=a₁+a₂+…+a_n（n∈N^*）．
  （1）求S₂₀₂₀的值；
  （2）求当

  k

  （

  k

  +

  1

  ）

  2

  ＜

  n

  ≤

  （

  k

  +

  1

  ）

  （

  k

  +

  2

  ）

  2

  （k∈N^*），试用n、k的代数式表示S_n（n∈N^*）；
  （3）对于t∈N^*，定义集合P_t={n|S_n是a_n的整数倍，n∈N^*，且1≤n≤t}，求集合P₂₀₂₀中元素的个数．
  组卷：49引用：3难度：0.4

  解析