当前位置：试卷中心 > 试卷详情

2022-2023学年黑龙江省齐齐哈尔市恒昌中学高二（上）期中数学试卷

发布：2024/9/3 5:0:8

一、选择题（每小题5分，共8小题40分）

1．椭圆
x
2
16
+
y
2
25
=
1
上点P到右焦点的距离为4，则点P到左焦点的距离为（　　）
A．6 B．3 C．4 D．2
组卷：11引用：4难度：0.7
解析
2．直线l的一个方向向量为（4，2，3），平面α的一个法向量为（2，1，t），若l⊥α，则实数t=（　　）
A．
3
2
B．1 C．-2 D．
-
8
3
组卷：25引用：4难度：0.7
解析
3．直线（a-1）x-（a+1）y+2=0恒过定点（　　）
A．（1，1） B．（1，-1） C．（-1，1） D．（-1，-1）
组卷：1031引用：4难度：0.7
解析
4．唐代诗人李顾的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河”，诗中隐含着一个有趣的数学问题--“将军饮马”问题，即将军在观望烽火之后从山脚下某处出发，先到河边饮马后再回到军营，怎样走才能使总路程最短？在平面直角坐标系中，设军营所在的位置为A（1，1），若将军从山脚下的点B（4，4）处出发，河岸线所在直线l的方程为x-y+1=0，则“将军饮马”的最短总路程是（　　）
A．3
6
B．
34
C．
5
D．2
5
组卷：223引用：4难度：0.7
解析
5．已知圆C：x²+y²+2x+4y+4=0，则圆上的点到坐标原点的距离的最大值为（　　）
A．
5
B．6 C．
5
-
1
D．
5
+
1
组卷：31引用：4难度：0.6
解析
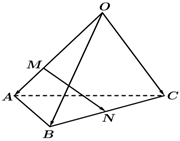6．如图所示，在四面体O-ABC中，
OA
=
a
，
OB
=
b
，
OC
=
c
，点M在OA上，且
OM
=2
MA
，N为BC的中点，则
MN
=（　　）
A．
1
2
a
-
2
3
b
+
1
2
c
B．-
2
3
a
+
1
2
b
+
1
2
c
C．
1
2
a
+
1
2
b
-
2
3
c
D．
2
3
a
+
2
3
b
-
1
2
c
组卷：1249引用：41难度：0.9
解析
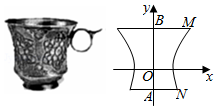7．如图为陕西博物馆收藏的国宝——唐•金筐宝钿团花纹金杯，杯身曲线内收，玲珑娇美，巧夺天工，是唐朝金银细作的典范之作．该杯的主体部分可以近似看作是双曲线
C
：
x
2
a
2
-
y
2
b
2
=1（a＞0，b＞0）的右支与y轴及平行于x轴的两条直线围成的曲边四边形ABMN绕y轴旋转一周得到的几何体，若该金杯主体部分的上口外直径为
10
3
3
，下底座外直径为
2
39
3
，且杯身最细之处到上杯口的距离是到下底座距离的2倍，则杯身最细之处的周长为（　　）
A．2
2
π B．3π C．2
3
π D．4π
组卷：104引用：4难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（第17小题10分，第18-22小题，每小题10分，共6小题70分）

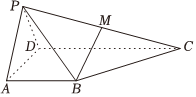21．如图所示，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，△PAD为等边三角形，
AB
=
AD
=
1
2
CD
，AB⊥AD，AB∥CD，点M是PC的中点，
（1）求平面PBC与平面BCD夹角的余弦值；
（2）在线段PB上是否存在一点N，使得DN⊥平面PBC？若存在，求出
PN
PB
的值；若不存在，请说明理由．
组卷：3引用：2难度：0.5
解析
22．如图，已知椭圆
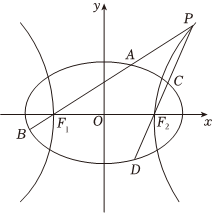x
2
a
2
+
y
2
b
2
=1（a＞b＞0）的离心率为
2
2
，以该椭圆上的点和椭圆的左、右焦点F₁，F₂为顶点的三角形的周长为4（
2
+1），一等轴双曲线的顶点是该椭圆的焦点，设P为该双曲线上异于顶点的任一点，直线PF₁和PF₂与椭圆的交点分别为A、B和C、D．
（Ⅰ）求椭圆和双曲线的标准方程；
（Ⅱ）设直线PF₁、PF₂的斜率分别为k₁、k₂，证明：k₁•k₂=1；
（Ⅲ）（此小题仅理科做）是否存在常数λ，使得|AB|+|CD|=λ|AB|•|CD|恒成立？若存在，求λ的值；若不存在，请说明理由．
组卷：1826引用：32难度：0.1
解析