2022-2023学年河南省郑州市高二（下）期末数学试卷

一、单选题：本大题共12个小题，每小题5分，共60分．在每小题所给出的四个选项中，只有一项是符合题目要求的．

• 1．已知数列{a_n}，满足a_n-a_n-1=2，a₁=0，则a₁₀=（　　）

  A．18

  B．36

  C．72

  D．144
  组卷：44引用：1难度：0.8

  解析

• 2．2023年5月10日，第七届全球跨境电子商务大会在郑州举行，小郑同学购买了几件商品，这些商品的价格如果按美元计，则平均数为30，方差为60，如果按人民币计（汇率按1美元=7元人民币），则平均数和方差分别为（　　）

  A．30，60

  B．30，420

  C．210，420

  D．210，2940
  组卷：24引用：1难度：0.8

  解析

• 3．如图，洛书古称龟书，是阴阳五行术数之源．在古代传说中有神龟出于洛水，其甲壳上有此图像，结构是戴九履一，左三右七，二四为肩，六八为足，以五居中，五方白圈皆阳数，四角黑点为阴数．若从四个阴数和五个阳数中随机选取4个数，则选取的4个数之和为奇数的方法数为（　　）

  A．60

  B．61

  C．65

  D．66
  组卷：39引用：3难度：0.6

  解析

• 4．下列四个命题中，正确命题的个数为（　　）
  ①甲乙两组数据分别为：甲：28，31，39，42，45，55，57，58，66；；乙：，29，34，35，48，42，46，55，53，55，67．则甲乙的中位数分别为45和44．
  ②相关系数r=-0.89，表明两个变量的相关性较弱．
  ③若由一个2×2列联表中的数据计算得K²的观测值k≈7.103，那么有99%的把握认为两个变量有关．
  ④用最小二乘法求出一组数据（x_i，y_i），（i=1，…，n）的回归直线方程

  ̂

  y

  =

  ̂

  b

  x

  +

  ̂

  a

  后要进行残差分析，相应于数据（x_i，y_i），（i=1，…，n）的残差是指

  ˆ

  e

  i

  =

  y

  i

  -

  （

  b

  x

  i

  +

  ̂

  a

  ）

  ．
  

  P（K2≥k0）	0.10	0.05	0.025	0.010	0.005	0.001
  k0	2.706	3.841	5.024	6.635	7.879	10.828

  A．1

  B．2

  C．3

  D．4
  组卷：60引用：1难度：0.5

  解析

• 5．已知（x-1）ⁿ的二项展开式的奇数项二项式系数和为64，若（x-1）ⁿ=a₀+a₁（x+1）+a₂（x+1）²+…+a_n（x+1）ⁿ，则a₁等于（　　）

  A．192

  B．448

  C．-192

  D．-448
  组卷：123引用：2难度：0.7

  解析

• 6．已知函数f（x）=ax²-lnx的图象在点（1，f（1））处的切线与直线y=3x平行，则该切线的方程为（　　）

  A．x-3y+5=0

  B．3x-y-1=0

  C．3x-y+1=0

  D．x-3y+1=0
  组卷：52引用：3难度：0.7

  解析

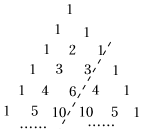• 7．“杨辉三角”是中国古代重要的数学成就，它比西方的“帕斯卡三角形”早了300多年．如图所示的是由“杨辉三角”拓展而成的三角形数阵，图中虚线上的数1，3，6，10…构成数列{a_n}，记a_n为该数列的第n项，则a₆₄=（　　）

  A．2016

  B．2080

  C．4032

  D．4160
  组卷：23引用：2难度：0.6

  解析

三、解答题：共70分．解答题应写出文字说明、证明过程或验算步骤．

• 21．根据长期生产经验，某种零件的一条生产线在设备正常状态下，生产的产品正品率为0.985．为了监控该生产线生产过程，检验员每天从该生产线上随机抽取10个零件，并测量其质量，规定：抽检的10件产品中，若至少出现2件次品，则认为设备出现了异常情况，需对设备进行检测及修理．
  （Ⅰ）假设设备正常状态，记X表示一天内抽取的10件产品中的次品件数，求P（X≥2），并说明上述监控生产过程规定的合理性；
  （Ⅱ）该设备由甲、乙两个部件构成，若两个部件同时出现故䧐，则设备停止运转；若只有一个部件出现故障，则设备出现异常．已知设备出现异常是由甲部件故障造成的概率为p,由乙部件故障造成的概率为1-p.若设备出现异常，需先检测其中一个部件，如果确认该部件出现故障，则进行修理，否则，继续对另一部件进行检测及修理．已知甲部件的检测费用2000元，修理费用6000元，乙部件的检测费用3000元，修理费用4000元．当设备出现异常时，仅考虑检测和修理总费用，应先检测甲部件还是乙部件，请说明理由．
  参考数据：0.985¹⁰≈0.86，0.985⁹≈0.87，0.985⁸≈0.89．
  组卷：32引用：3难度：0.6

  解析

• 22．已知函数f（x）=lnx+

  1

  x

  ．
  （Ⅰ）求函数f（x）的最小值；
  （Ⅱ）设函数g（x）=f（x）-

  a

  x

  2

  +

  x

  -

  a

  x

  2

  ．证明：当0＜a＜

  1

  2

  时，∀x∈

  （

  0

  ，

  a

  1

  -

  a

  ）

  ，g（x）＞0恒成立．
  组卷：40引用：1难度：0.6

  解析