2021-2022学年上海市闵行区七宝中学高一（下）期末数学试卷

一、填空题。（本大题共有12小题，满分54分，第1-6题每题4分，第7-12题每题5分）

• 1．三条互相平行的直线最多可确定

  个平面．
  组卷：208引用：4难度：0.7

  解析

• 2．若复数z满足（3-4i）z=|4+3i|，则z的虚部为

  ．
  组卷：320引用：19难度：0.7

  解析

• 3．若圆锥的侧面展开图是半径为4的半圆，则此圆锥的体积为

  ．
  组卷：109引用：9难度：0.5

  解析

• 4．将复数化为三角形式：

  1

  2

  -

  1

  2

  i

  =

  ．
  组卷：115引用：3难度：0.6

  解析

• 5．若正四棱柱ABCD-A₁B₁C₁D₁的底面边长为1，直线AC₁与底面ABCD所成角的大小是60°，则A₁C₁到底面ABCD的距离为

  ．
  组卷：22引用：2难度：0.6

  解析

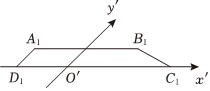• 6．如图所示，梯形A₁B₁C₁D₁是水平放置的平面图形ABCD的直观图（斜二测画法），若A₁D₁∥O'y'，A₁B₁∥C₁D₁，A₁B₁=

  2

  3

  C

  1

  D

  1

  =4，A₁D₁=1，则四边形ABCD的面积是

  ．
  组卷：21引用：2难度：0.7

  解析

• 7．正四棱锥的相邻两侧面所成二面角的大小的取值范围是

  ．
  组卷：15引用：2难度：0.5

  解析

三、解答题。（本大题共5题，满分76分）

• 20．对于任意的复数z=x+yi（x,y∈R），定义运算P（z）=x²[cos（yπ）+isin（yπ）]．
  （1）集合A={ω|ω=P（z），|z|≤1，Rez,Imz均为整数}，试用列举法写出集合A；
  （2）若z=2+yi（y∈R），P（z）为纯虚数，求|z|的最小值；
  （3）直线l：y=x-9上是否存在整点（x,y）（坐标x,y均为整数的点），使复数z=x+yi经运算P后，P（z）对应的点也在直线l上？若存在，求出所有的点；若不存在，请说明理由．
  组卷：602引用：3难度：0.1

  解析

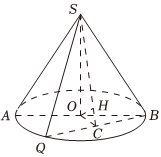• 21．圆锥的轴截面为等腰Rt△SAB，Q为底面圆周上一点．
  （1）若QB的中点为C，OH⊥SC，求证：OH⊥平面SQB；
  （2）如果∠AOQ=60°，

  QB

  =

  2

  3

  ，求此圆锥的侧面积；
  （3）如果二面角A-SB-Q的大小为

  arctan

  （

  2

  -

  2

  ）

  ，求∠AOQ的大小．
  组卷：12引用：2难度：0.4

  解析