2022-2023学年浙江省杭州十四中高一（下）期中数学试卷

一．选择题：本大题共8小题，每小题5分，共40分．每小题列出的四个选项中只有一个是符合题目要求的，不选、多选、错选均不得分.

• 1．复数

  z

  =

  3

  +

  i

  1

  +

  i

  在复平面上对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：59引用：4难度：0.8

  解析

• 2．“a＞b”是“lga＞lgb”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：128引用：8难度：0.8

  解析

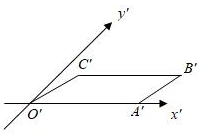• 3．如图，平行四边形O'A'B'C'是水平放置的一个平面图形的直观图，其中O'A'=5，O'C'=2，∠A'O'C'=30°，则原图形的面积是（　　）

  A．4

  B． 4 2

  C． 10 2

  D．6
  组卷：335引用：4难度：0.9

  解析

• 4．已知l是直线，α、β是两个不同平面，下列命题中的真命题是（　　）

  A．若l∥α，l∥β，则α∥β	B．若α⊥β，l∥α，则l⊥β
  C．若l⊥α，l∥β，则α⊥β	D．若l∥α，α∥β，则l∥β
  组卷：272引用：13难度：0.9

  解析

• 5．在△ABC中，点D在边BC的延长线上，且

  BC

  =

  3

  CD

  ．若

  AO

  =

  x

  AB

  +

  （

  1

  -

  x

  ）

  AC

  ，-

  1

  3

  ＜x＜0，则点O在（　　）

  A．线段BC上

  B．线段CD上

  C．线段AC上

  D．线段AD上
  组卷：157引用：5难度：0.6

  解析

• 6．如表为某港口在某季节中每天水深与时刻的关系：
  

  时刻	0：00	3：00	6：00	9：00	12：00	15：00	18：00	21：00	24：00
  水深（单位：m）	5	7	5	3	5	7	5	3	5

  若该港口水深y（单位：m）和时刻t（0≤t≤24）的关系可用函数y=Asin（ωt+φ）+h来近似描述，则该港口在11：00的水深（单位：m）为（　　）

  A．4

  B．5 - 2

  C．5- 3

  D．3- 3
  组卷：35引用：2难度：0.6

  解析

• 7．在直三棱柱ABC-A₁B₁C₁中，

  AB

  =

  4

  ，

  BC

  =

  AC

  =

  2

  2

  ，

  A

  A

  1

  =

  1

  ，点M，N分别是A₁B₁，A₁C₁的中点，则直线BM与CN所成角的余弦值为（　　）

  A． 15 5

  B． 10 5

  C． 5 3

  D． 6 3
  组卷：276引用：4难度：0.7

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤.

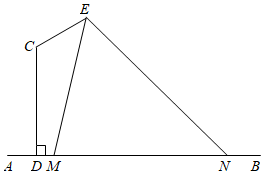• 21．我校在一条水泥路边安装路灯，其中灯杆的设计如图所示，AB为底面，CD、CE为路灯的灯杆，CD⊥AB，且

  ∠

  DCE

  =

  2

  3

  π

  ，在E处安装路灯，且路灯的照明张角为

  ∠

  MEN

  =

  π

  3

  ，已知CD=5米，CE=3米．
  （1）当M与D重合时，求路灯在路面的照明宽度MN；
  （2）求此路灯在路面上的照明宽度MN的最小值．
  组卷：194引用：3难度：0.6

  解析

• 22．若在定义域内存在实数x₀，使得f（x₀+1）=f（x₀）+f（1）成立，则称函数有“飘移点”x₀．
  （1）函数

  f

  （

  x

  ）

  =

  1

  x

  是否有“飘移点”？请说明理由；
  （2）证明函数f（x）=x²+2^x在（0，1）上有“飘移点”；
  （3）若函数

  f

  （

  x

  ）

  =

  lg

  （

  a

  x

  2

  +

  1

  ）

  在（0，1）上有“飘移点”，求实数a的取值范围．
  组卷：53引用：2难度：0.5

  解析