当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省徐州一中高一（下）期中数学试卷

发布：2024/7/17 8:0:9

一、单选题：本题共8小题，每小题5分，共40分.在每小题的四个选项中，只有一项符合题目要求.

1．已知复数z满足z（2+i）=2-i,其中i为虚数单位，则
z
•
z
=（　　）
A．
1
3
B．
1
2
C．1 D．2
组卷：28引用：2难度：0.8
解析
2．已知在如图所示的等腰梯形ABCD中，AB=1，DC=3，
AD
=
2
，用斜二测画法画出该梯形的直观图，则该梯形的直观图的面积为（　　）
A．
2
4
B．
2
2
C．2 D．
8
2
组卷：111引用：4难度：0.8
解析
3．已知向量
a
=
（
2
，
1
）
，
b
=
（
2
，-
2
）
，向量
a
在向量
b
上的投影向量的坐标为（　　）
A．（2，-2） B．
（
1
2
，-
1
2
）
C．
（
2
5
，
1
5
）
D．
（
2
2
，-
2
2
）
组卷：172引用：4难度：0.8
解析
4．已知
tan
（
α
-
π
6
）
=
2
，tan（α+β）=-3，则
tan
（
β
+
π
6
）
=（　　）
A．1 B．2 C．3 D．4
组卷：1098引用：12难度：0.7
解析
5．圆木长1丈5尺，圆周为4尺，葛藤从圆木的底部开始向上生长，绕圆木两周，刚好顶部与圆木平齐，问葛藤最少长多少尺？这个问题的答案为（注：1丈等于10尺）（　　）
A．18尺 B．17尺 C．16尺 D．15尺
组卷：11引用：2难度：0.5
解析
6．已知锐角△ABC的内角A，B，C的对边分别为a,b,c,若
a
=
3
，b²+c²-bc=3，则△ABC面积的取值范围是（　　）
A．
（
3
2
，
3
3
4
]
B．
（
3
2
，
3
3
4
）
C．
（
3
4
，
3
3
4
）
D．
（
3
4
，
3
3
4
]
组卷：696引用：9难度：0.7
解析
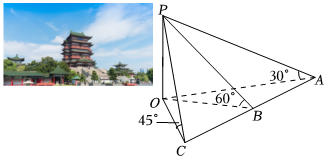7．滕王阁，江南三大名楼之一，因初唐诗人王勃所作《滕王阁序》中的“落霞与孤鹜齐飞，秋水共长天一色”而名传千古，流芳后世．如图，在滕王阁旁地面上共线的三点A，B，C处测得阁顶端点P的仰角分别为30°，60°，45°，且AB=BC=70米，则滕王阁的高度OP=（　　）米．
A．
14
15
B．
15
15
C．
68
15
5
D．
29
15
2
组卷：55引用：2难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，第17题10分，第18-22题各12分，共70分.解答应写出文字说明、证明过程或演算步骤.

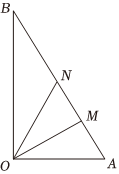21．如图，某镇有一块空地△OAB，其中OA=3km,
OB
=
3
3
km
，∠AOB=90°．当地镇政府计划将这块空地改造成一个旅游景点，拟在中间挖一个人工湖△OMN，其中M，N都在边AB上且不与端点重合，且∠MON=30°，挖出的泥土堆放在△OBN地带上形成假山，剩下的△OAM地带设儿童游乐场，为了安全起见，需在△OBM的周围安装防护网．
（1）当BN=3km时，求防护网的总长度；
（2）为节省投入资金，人工湖△OMN的面积要尽可能小，问：∠BON多大时，可使△OMN的面积最小？最小面积是多少？
组卷：127引用：2难度：0.6
解析
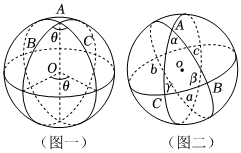22．如图一：球面上的任意两个与球心不在同一条直线上的点和球心确定一个平面，该平面与球相交的图形称为球的大圆，任意两点都可以用大圆上的劣弧进行连接．过球面一点的两个大圆弧，分别在弧所在的两个半圆内作公共直径的垂线，两条垂线的夹角称为这两个弧的夹角．
如图二：现给出球面上三个点，其任意两个不与球心共线，将它们两两用大圆上的劣弧连起来的封闭图形称为球面三角形．两点间的弧长定义为球面三角形的边长，两个弧的夹角定义为球面三角形的角．
现设图二球面三角形ABC的三边长为a,b,c,三个角大小为α，β，γ，球的半径为R．
（1）求证：a+b＞c
（2）①求球面三角形ABC的面积S（用α，β，γ，R表示）．
②证明：α+β+γ＞π．
组卷：41引用：3难度：0.6
解析