菁于教，优于学

申请校本题库

试卷征集

加入会员

操作视频

当前位置：试卷中心 > 试卷详情

2022-2023学年山东省临沂一中文峰校区高一（下）月考数学试卷（4月份）

发布：2024/7/15 8:0:9

一、单选题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

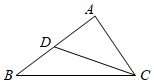1．如图所示，D是△ABC的边AB上的中点，记
BC
=
a
，
BA
=
c
，则向量
CD
=（　　）
A．
-
a
-
1
2
c
B．
-
a
+
1
2
c
C．
a
-
1
2
c
D．
a
+
1
2
c
组卷：399引用：13难度：0.9
解析
2．计算
1
-
tan
15
°
1
+
tan
15
°
=（　　）
A．
-
3
B．
3
C．
-
3
3
D．
3
3
组卷：223引用：5难度：0.8
解析
3．已知△ABC是边长为2的等边三角形，则
CA
•
AB
=（　　）
A．-2 B．
-
2
3
C．2 D．
2
3
组卷：85引用：3难度：0.8
解析
4．已知
|
a
|
=
4
，
|
b
|
=
3
，
（
2
a
-
3
b
）
•
（
2
a
+
b
）
=
13
，求
a
与
b
的夹角θ=（　　）
A．
π
6
B．
π
4
C．
π
3
D．
2
π
3
组卷：94引用：3难度：0.8
解析
5．已知sin（α-
π
6
）=
1
3
，则sin（2
α
+
π
6
）=（　　）
A．
7
9
B．-
7
9
C．
2
9
D．-
2
9
组卷：604引用：11难度：0.8
解析
6．若平面向量
a
，
b
，
c
两两的夹角相等，且
|
a
|
=
2
，
|
b
|
=
2
，
|
c
|
=
3
，则
|
a
+
b
+
2
c
|
=（　　）
A．2 B．10 C．5或2 D．10或4
组卷：47引用：3难度：0.7
解析
7．已知△ABC的外接圆圆心为O，且
2
AO
=
AB
+
AC
，
|
OA
|
=
|
AB
|
，则向量
CA
在向量
BC
上的投影向量为（　　）
A．
1
4
BC
B．
3
4
BC
C．
-
1
4
BC
D．
-
3
4
BC
组卷：124引用：5难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题．共70分．解答应写出文字说明，证明过程或演算步骤．

21．已知
m
=
（
3
sinx
,-
1
）
，
n
=
（
cosx
,
cos
2
x
+
1
2
）
，设函数
f
（
x
）
=
m
•
n
．
（1）当
x
∈
[
-
π
12
，
5
π
12
]
时，求函数f（x）的最值及取得最值时的x；
（2）设△ABC的内角A，B，C的对边分别是a,b,c,且
a
=
2
3
，b=6，
f
（
A
2
）
=
-
1
，求c的值．
组卷：35引用：1难度：0.6
解析
22．在△ABC中，角A，B，C的对边分别为a,b,c,且b=a（sinC+cosC）．
（1）求A；
（2）在
①
a
=
2
，
②
B
=
π
3
，
③
c
=
2
b
这三个条件中，选出两个使△ABC唯一确定的条件补充在下面的问题中，并解答问题，若____，____，求△ABC的面积．
组卷：276引用：5难度：0.6
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

商务合作服务条款走进菁优

帮助中心兼职招聘意见反馈

深圳市菁优智慧教育股份有限公司

粤ICP备10006842号公网安备44030502001846号

©2010-2025 jyeoo.com 版权所有

深圳市市场监管
主体身份认证

APP开发者：深圳市菁优智慧教育股份有限公司| 应用名称：菁优网 | 应用版本：5.0.7 |隐私协议|第三方SDK|用户服务条款

广播电视节目制作经营许可证|出版物经营许可证|网站地图

本网部分资源来源于会员上传，除本网组织的资源外，版权归原作者所有，如有侵犯版权，请立刻和本网联系并提供证据，本网将在三个工作日内改正