当前位置：试卷中心 > 试卷详情

2021-2022学年北京五十七中高二（上）月考数学试卷（10月份）

发布：2024/8/30 9:0:8

一、选择题（共10个小题，每题4分，共40分）

1．若复数（1-i）（a+i）在复平面内对应的点在第二象限，则实数a的取值范围是（　　）
A．（-∞，1） B．（-∞，-1） C．（1，+∞） D．（-1，+∞）
组卷：5212引用：39难度：0.9
解析
2．下列函数中，为偶函数且有最小值的是（　　）
A．f（x）=x²+x B．f（x）=|lnx|
C．f（x）=xsinx D．f（x）=e^x+e^-x
组卷：74引用：4难度：0.9
解析
3．已知奇函数f（x）在R上是增函数．若a=-f（
lo
g
2
1
5
），b=f（log₂4.1），c=f（2^0.8），则a,b,c的大小关系为（　　）
A．a＜b＜c B．b＜a＜c C．c＜b＜a D．c＜a＜b
组卷：9081引用：49难度：0.7
解析
4．已知m,n,l为三条不同的直线，α，β，γ为三个不同的平面，有以下结论：
①若m⊥l,n⊥l,则m∥n
②若α⊥γ，β⊥γ，则α∥β
③若m∥α，m⊥n,则n⊥α
④若m⊥α，m⊥n,则n∥α
⑤若m⊥n,m⊥α，n⊥β，则α⊥β
⑥若l∥α，l⊥β，则α⊥β
其中正确结论的个数是（　　）
A．1 B．2 C．3 D．4
组卷：16引用：1难度：0.5
解析
5．已知长方体ABCD-A₁B₁C₁D₁中，
A
A
1
=
AB
=
3
，AD=1，则异面直线B₁C和C₁D所成角的余弦值为（　　）
A．
6
4
B．
6
3
C．
2
6
D．
3
6
组卷：377引用：6难度：0.9
解析
6．已知函数f（x）=
e
x
，
x
≤
0
lnx
,
x
＞
0
，g（x）=f（x）+x+a.若g（x）存在2个零点，则a的取值范围是（　　）
A．[-1，0） B．[0，+∞） C．[-1，+∞） D．[1，+∞）
组卷：9270引用：80难度：0.5
解析
7．两个圆锥的底面是一个球的同一截面，顶点均在球面上，若球的体积为
32
π
3
，两个圆锥的高之比为1：3，则这两个圆锥的体积之和为（　　）
A．3π B．4π C．9π D．12π
组卷：4698引用：9难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共6个题，满分80分）

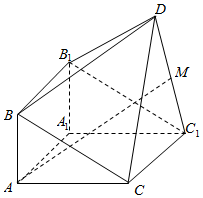21．如图，由直三棱柱ABC-A₁B₁C₁和四棱锥D-BB₁C₁C构成的几何体中，∠BAC=90°，AB=1，BC=BB₁=2，C₁D=CD=
5
，平面CC₁D⊥平面ACC₁A₁．
（Ⅰ）求证：AC⊥DC₁；
（Ⅱ）若M为DC₁中点，求证：AM∥平面DBB₁；
（Ⅲ）在线段BC上（含端点）是否存在点P，使直线DP与平面DBB₁所成的角为
π
3
？若存在，求
BP
BC
的值，若不存在，说明理由．
组卷：501引用：6难度：0.5
解析
22．设n为正整数，集合A={α|α=（t₁，t₂，…t_n），t_k∈{0，1}，k=1，2，…，n}，对于集合A中的任意元素α=（x₁，x₂，…，x_n）和β=（y₁，y₂，…y_n），记M（α，β）=
1
2
[（x₁+y₁-|x₁-y₁|）+（x₂+y₂-|x₂-y₂|）+…（x_n+y_n-|x_n-y_n|）]．
（Ⅰ）当n=3时，若α=（1，1，0），β=（0，1，1），求M（α，α）和M（α，β）的值；
（Ⅱ）当n=4时，设B是A的子集，且满足：对于B中的任意元素α，β，当α，β相同时，M（α，β）是奇数；当α，β不同时，M（α，β）是偶数．求集合B中元素个数的最大值；
（Ⅲ）给定不小于2的n,设B是A的子集，且满足：对于B中的任意两个不同的元素α，β，M（α，β）=0，写出一个集合B，使其元素个数最多，并说明理由．
组卷：1481引用：22难度：0.1
解析