2022-2023学年河南省焦作市武陟一中高二（下）期末数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．若集合A={x|2x²-7x+3≤0}，B={x|y=ln（2x-5）}，则（∁_RA）∪B=（　　）

  A． { x | 5 2 ＜ x ≤ 3 }	B． { x | 5 2 ≤ x ≤ 3 }
  C． { x | x ≥ 1 2 }	D．{x|x＜ 1 2 或x＜ 5 2 }
  组卷：49引用：1难度：0.8

  解析

• 2．若复数z满足（1-2i）•z=（2+i）²，

  z

  为z的共轭复数，则z

  •

  z

  =（　　）

  A． 5

  B．5

  C． 3

  D．3
  组卷：77引用：3难度：0.8

  解析

• 3．

  （

  x

  3

  +

  2

  ）

  （

  2

  x

  -

  1

  x

  2

  ）

  6

  的展开式中常数项为（　　）

  A．80

  B．160

  C．240

  D．320
  组卷：379引用：5难度：0.7

  解析

• 4．函数

  f

  （

  x

  ）

  =

  x

  3

  2

  |

  x

  |

  +

  x

  2

  的大致图象为（　　）

  A．	B．
  C．	D．
  组卷：49引用：3难度：0.7

  解析

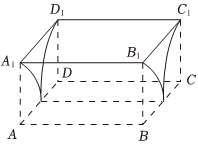• 5．在长方体ABCD-A₁B₁C₁D₁中，AB=6，AD=6，AA₁=3，现分别以AB，CD为轴，截去底面半径为3的两个四分之一圆柱，得到如图所示几何体，则该几何体的表面积为（　　）

  A．18π+54

  B．18π+72

  C．9π+72

  D．9π+54
  组卷：92引用：1难度：0.8

  解析

• 6．定义：[x]表示不大于x的最大整数已知函数

  f

  （

  x

  ）

  =

  [

  x

  ]

  x

  2

  -

  2

  x

  +

  1

  ，

  x

  ∈

  （

  0

  ，

  3

  ]

  ，则（　　）

  A．函数f（x）在（0，1]上单调递增

  B．函数f（x）的最大值为0

  C．函数f（x）在（0，3]上单调递减

  D．函数f（x）的最小值为 - 20 3
  组卷：142引用：1难度：0.4

  解析

• 7．已知F₁，F₂分别为双曲线C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的左、右焦点，点P在C上，若∠F₁PF₂=

  π

  3

  ，O为坐标原点，|OP|=2

  3

  且△F₁PF₂的面积为3

  3

  ，则双曲线C的渐近线方程为（　　）

  A．x±y=0

  B． 2 x ± y = 0

  C． 3 x±y=0

  D．2x±y=0
  组卷：91引用：1难度：0.5

  解析

四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知双曲线

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的右焦点为F（2，0），点F到C的渐近线的距离为1．
  （1）求C的方程．
  （2）若直线l₁与C的右支相切，切点为P，l₁与直线

  l

  2

  ：

  x

  =

  3

  2

  交于点Q，问x轴上是否存在定点M，使得MP⊥MQ？若存在，求出M点坐标；若不存在，请说明理由．
  组卷：105引用：2难度：0.5

  解析

• 22．已知函数f（x）=ln（1+x）+axe^-x．
  （1）当a=1时，求曲线y=f（x）在点（0，f（0））处的切线方程；
  （2）若f（x）在区间（-1，0），（0，+∞）各恰有一个零点，求a的取值范围．
  组卷：3547引用：6难度：0.2

  解析