2022-2023学年辽宁省沈阳二十中高二（上）第一次月考数学试卷

一、单项选择题（1-8题，每题5分，共40分）

• 1．直线l经过圆C：x²+y²-2x+2y+1=0的圆心C，且倾斜角为

  π

  6

  ，则直线l的方程为（　　）

  A． 3 x-y- 3 -1=0	B． 3 x-y+ 3 +1=0
  C． 3 x-3y+ 3 +3=0	D． 3 x-3y- 3 -3=0
  组卷：153引用：4难度：0.8

  解析

• 2．“a=1”是“直线x+ay-1=0与直线ax-y+1=0相互垂直”的（　　）

  A．充分而不必要条件	B．必要而不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：411引用：6难度：0.8

  解析

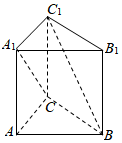• 3．如图，在直三棱柱ABC-AB₁C₁中，AC=3，BC=4，CC₁=3，∠ACB=90°，则BC₁与A₁C所成的角的余弦值为（　　）

  A． 3 3

  B． 3 2 10

  C． 2 4

  D． 5 5
  组卷：165引用：10难度：0.7

  解析

• 4．已知方程x²+y²-2x+2k+3=0表示圆，则k的取值范围是（　　）

  A．（-∞，-1）	B．（3，+∞）
  C．（-∞，-1）∪（3，+∞）	D．（- 3 2 ， + ∞ ）
  组卷：796引用：12难度：0.9

  解析

• 5．若过点（2，1）的圆与两坐标轴都相切，则圆心到直线2x-y-3=0的距离为（　　）

  A． 5 5

  B． 2 5 5

  C． 3 5 5

  D． 4 5 5
  组卷：2071引用：46难度：0.7

  解析

• 6．已知⊙M：x²+y²-2x-2y-2=0，直线l：2x+y+2=0，P为l上的动点．过点P作⊙M的切线PA，PB，切点为A，B，当|PM|•|AB|最小时，直线AB的方程为（　　）

  A．2x-y-1=0

  B．2x+y-1=0

  C．2x-y+1=0

  D．2x+y+1=0
  组卷：9700引用：34难度：0.5

  解析

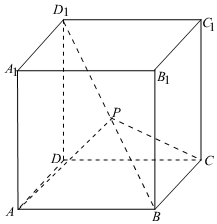• 7．已知动点P在正方体ABCD-A₁B₁C₁D₁的对角线BD₁（不含端点）上，设

  D

  1

  P

  D

  1

  B

  =λ，若∠APC为钝角，则实数λ的取值范围为（　　）

  A．（0， 1 3 ）

  B．（0， 1 2 ）

  C．（ 1 2 ，1）

  D．（ 1 3 ，1）
  组卷：221引用：8难度：0.6

  解析

四、解答题（共6小题，17题10分，其余每题12分）

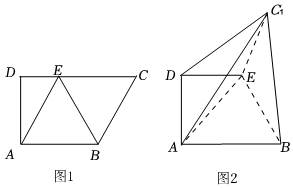• 21．图1是直角梯形ABCD，AB∥CD，∠D=90°，四边形ABCE是边长为2的菱形，并且∠BCE=60°，以BE为折痕将△BCE折起，使点C到达C₁的位置，且

  A

  C

  1

  =

  6

  ，如图2．
  （1）求证：平面BC₁E⊥平面ABED；
  （2）在棱DC₁上是否存在点P，使得P到平面ABC₁的距离为

  15

  5

  ？若存在，求出直线EP与平面ABC₁所成角的正弦值．
  组卷：1017引用：10难度：0.4

  解析

• 22．已知圆C：（x-2）²+y²=1，点P是直线l：x+y=0上一动点，过点P作圆C的切线PA，PB，切点分别是A和B．
  （1）试问直线AB是否恒过定点，若是，求出这个定点，若否说明理由；
  （2）直线x-y+m=0与圆C交于E，F两点，求

  OE

  •

  OF

  的取值范围（O为坐标原点）．
  组卷：210引用：3难度：0.5

  解析