2022-2023学年浙江省台州市八校联盟高一(下)期中数学试卷
发布:2024/5/13 8:0:8
一、单项选择题:本大题共8小题,每小题5分,共40分.每个小题给出的四个备选项中只有一项是符合题目要求的,不选、多选、错选均不得分.
-
1.已知复数z=i2+(k+1)i+k是纯虚数,则实数k=( )
组卷:38引用:2难度:0.9 -
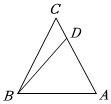 2.如图,在△ABC中,AD=2DC,若,BA=a,则BC=b=( )BD组卷:326引用:5难度:0.8
2.如图,在△ABC中,AD=2DC,若,BA=a,则BC=b=( )BD组卷:326引用:5难度:0.8 -
3.已知空间中点A,B,直线l,平面α,若A∈l,B∈l,A∉α,B∈α,则下列结论正确的是( )
组卷:101引用:1难度:0.9 -
4.在△ABC中,角A,B,C所对的边分别是a,b,c,若A=60°,B=45°,a=3,则b=( )
组卷:456引用:8难度:0.7 -
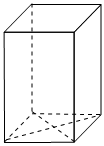 5.如图,已知一个直四棱柱的侧棱长为6,底面是对角线长分别是9和13的菱形,则这个四棱柱的侧面积是( )组卷:153引用:1难度:0.8
5.如图,已知一个直四棱柱的侧棱长为6,底面是对角线长分别是9和13的菱形,则这个四棱柱的侧面积是( )组卷:153引用:1难度:0.8 -
6.在△ABC中,M为边BC上的任意一点,点N在线段AM上,且满足
=AN13,若NM=λAN+μAB(λ,μ∈R),则λ+μ的值为( )AC组卷:315引用:5难度:0.5 -
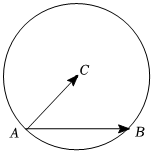 7.如图,在圆C中,AC=5,点A,B在圆上,AB=4,则的值为( )AB•AC组卷:77引用:1难度:0.8
7.如图,在圆C中,AC=5,点A,B在圆上,AB=4,则的值为( )AB•AC组卷:77引用:1难度:0.8
四、解答题:本题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
20.已知在△ABC中,角A,B,C所对的边为a,b,c,且满足
.2sinA+22cosA-2=1-cos2Ccos(π2+2C)
(1)判断角B与角C的关系,并说明理由;
(2)若,求B∈(π4,π3]的范围.cb组卷:66引用:1难度:0.5 -
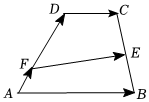 21.如图,梯形ABCD,AB=2DC=4,∠ADC=π,E为BC的中点,F是AD上的任意一点,设23.AF=λAD
21.如图,梯形ABCD,AB=2DC=4,∠ADC=π,E为BC的中点,F是AD上的任意一点,设23.AF=λAD
(1)当F是AD的三等分点时,试用向量,AD表示向量DC;FE
(2)若,求证:||AD|=t(t>0)|的最小值与t无关.FE组卷:42引用:1难度:0.6


