2022-2023学年江苏省常州市金坛区华罗庚中学创新班高一（下）期末数学试卷

一、单选题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知复数z满足

  z

  =

  2

  1

  -

  i

  +

  i

  ，则|z|=（　　）

  A．1

  B． 2

  C． 3

  D． 5
  组卷：297引用：13难度：0.8

  解析

• 2．已知△ABC中，AB=5，BC=7，CA=9，则∠CAB∈（　　）

  A． （ π 6 ， π 5 ）

  B． （ π 5 ， π 4 ）

  C． （ π 4 ， π 3 ）

  D． （ π 3 ， π 2 ）
  组卷：166引用：4难度：0.8

  解析

• 3．已知直线l₁：x+ay+2=0，l₂：2x+4y+3=0相互平行，则l₁、l₂之间的距离为（　　）

  A． 5 10

  B． 5 5

  C． 2 5 5

  D． 5 2
  组卷：582引用：3难度：0.8

  解析

• 4．一个圆台的上底面半径为1，下底面半径为2，高为2，以该圆台的上底面为底面，挖去一个半球，则剩余部分几何体的体积为（　　）

  A． 11 3 π

  B． 10 3 π

  C．4π

  D．3π
  组卷：144引用：4难度：0.7

  解析

• 5．若直线x+ay-a-2=0与圆C：（x-2）²+y²=4交于A，B两点，当|AB|最小时，劣弧

  ˆ

  AB

  的长为（　　）

  A． π 2

  B． 4 π 3

  C． 2 π 3

  D．π
  组卷：134引用：3难度：0.7

  解析

• 6．在四棱锥P-ABCD中，四边形ABCD为正方形，PA⊥平面ABCD，且PA=6，AB=8，则四棱锥P-ABCD的外接球与内切球的表面积之比为（　　）

  A． 41 2

  B． 41 4

  C．3

  D． 11 2
  组卷：578引用：6难度：0.4

  解析

• 7．在如图所示的长方体ABCD-A₁B₁C₁D₁中AB=2，AD=3，AA₁=4，点M为棱AA₁的中点，若N为底面A₁B₁C₁D₁内一点，满足MN∥面BDC₁，设直线MN与直线CC₁所成角为α，则tanα的取值范围是（　　）

  A． [ 3 4 ， 3 13 13 ]

  B． [ 3 4 ， 3 13 13 ）

  C． [ 3 26 13 ， 3 4 ]

  D． [ 3 26 13 ， 1 2 ]
  组卷：183引用：4难度：0.5

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．在△ABC中，内角A，B，C的对边分别为a,b,c,

  cos

  A

  cos

  C

  =

  -

  3

  a

  2

  b

  +

  3

  c

  ，点D是边BC上的一点，且

  sin

  ∠

  BAD

  b

  +

  sin

  ∠

  CAD

  c

  =

  3

  2

  a

  ．
  （1）求证：

  AD

  =

  a

  3

  ；
  （2）若CD=2BD，求cos∠ADC．
  组卷：323引用：5难度：0.4

  解析

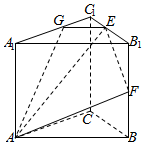• 22．在棱长均为2的正三棱柱ABC-A₁B₁C₁中，E为B₁C₁的中点．过AE的截面与棱BB₁，A₁C₁分别交于点F，G．
  （1）若F为BB₁的中点，求三棱柱被截面AGEF分成上下两部分的体积比

  V

  1

  V

  2

  ；
  （2）若四棱锥A₁-AGEF的体积为

  7

  3

  12

  ，求截面AGEF与底面ABC所成二面角的正弦值；
  （3）设截面AFEG的面积为S₀，△AEG面积为S₁，△AEF面积为S₂，当点F在棱BB₁上变动时，求

  S

  2

  0

  S

  1

  S

  2

  的取值范围．
  组卷：477引用：6难度：0.3

  解析