2022-2023学年山东省青岛市莱西市高一（下）期末数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．下列四个命题中，正确的个数为（　　）
  ①满足z=

  1

  z

  的复数，只有±1；
  ②若a,b∈R，且a=b,则（a-b）+（a+b）i是纯虚数；
  ③复数z∈R的充要条件是z=

  z

  ；
  ④复平面内，x轴是实轴，y轴是虚轴．

  A．0个

  B．1个

  C．2个

  D．3个
  组卷：47引用：1难度：0.7

  解析

• 2．若直线m不平行于平面α，且m⊄α，则下列结论成立的是（　　）

  A．α内不存在与m异面的直线

  B．α内存在与m平行的直线

  C．α内存在唯一一条直线与m相交

  D．α内存在与m垂直的直线
  组卷：40引用：2难度：0.7

  解析

• 3．如果一组数据的中位数比平均数小很多，则下列叙述一定错误的是（　　）

  A．数据中可能有异常值

  B．这组数据是近似对称的

  C．数据中可能有极端大的值

  D．数据中众数可能和中位数相同
  组卷：102引用：4难度：0.7

  解析

• 4．抛掷两枚质地均匀的硬币，设事件M=“第一枚硬币正面朝上”，事件N=“第二枚硬币反面朝上”，则下列结论中正确的为（　　）

  A．M与N互为对立事件	B．M与N互斥
  C．P（M）=P（N）	D．M与N相等
  组卷：56引用：1难度：0.8

  解析

• 5．为了得到函数

  y

  =

  sin

  2

  x

  -

  3

  cos

  2

  x

  的图象，只需把函数

  y

  =

  sin

  （

  2

  x

  +

  π

  6

  ）

  的图象上的所有点（　　）

  A．向左平移 3 π 4 个单位长度，然后把图象上各点的坐标纵坐标伸长到原来的2倍

  B．向右平移 π 4 个单位长度，然后再把图象上各点的纵坐标缩短到原来的 1 2 倍

  C．向左平移 π 4 个单位长度，然后再把图象上各点的纵坐标伸长到原来的2倍

  D．向右平移 3 π 4 个单位长度，然后再把图象上每点的纵坐标缩短到原来的 1 2 倍
  组卷：533引用：3难度：0.8

  解析

• 6．已知A（-1，2），B（3，0），点P在直线AB上，且

  |

  AP

  |

  =

  2

  |

  PB

  |

  ，则点P的坐标为（　　）

  A． （ 5 3 ， 2 3 ） 或（7，-2）	B． （ 5 3 ， 2 3 ）
  C．（2，1）或（7，-2）	D．（7，2）
  组卷：170引用：5难度：0.8

  解析

• 7．对于△ABC，若存在△A₁B₁C₁，满足

  cos

  A

  sin

  A

  1

  =

  cos

  B

  sin

  B

  1

  =

  cos

  C

  sin

  C

  1

  =

  1

  ，则称△ABC为“V类三角形”，V类三角形一定满足（　　）

  A．有一个内角为30°	B．有一个内角为60°
  C．有一个内角为75°	D．有一个内角为45°
  组卷：31引用：1难度：0.9

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

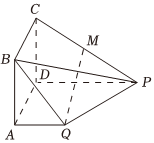• 21．如图，四边形ABCD是边长为2的正方形，PD⊥平面ABCD，PD∥AQ，且PD=2AQ，M为PC的中点．
  （Ⅰ）求证：PD⊥QM；
  （Ⅱ）设平面PBQ∩平面ABCD=l,l与直线QM所成的角为θ，求tanθ．
  组卷：108引用：1难度：0.5

  解析

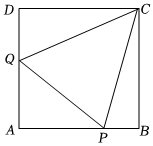• 22．如图，正方形ABCD的边长为1，P，Q分别为边AB，AD上的点，△APQ的周长为2．
  （Ⅰ）求∠PCQ的大小；
  （Ⅱ）设∠BCP=α，W=

  1

  C

  P

  2

  +

  1

  C

  Q

  2

  ，试将W表示为α的函数，并求出W的最大值及相应的α．
  组卷：32引用：1难度：0.6

  解析